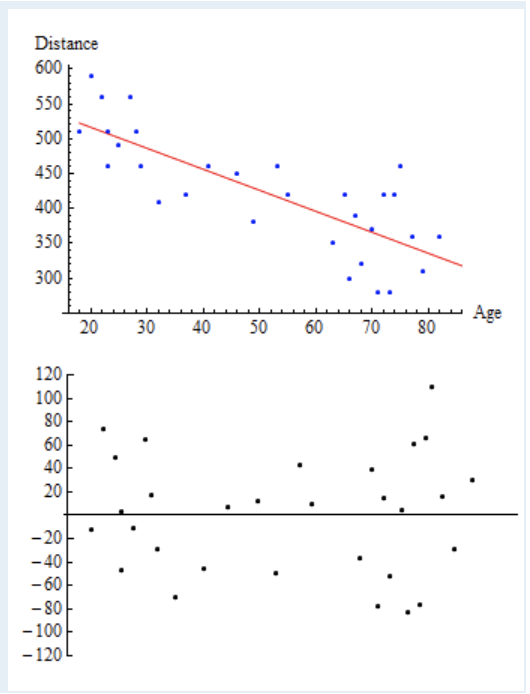
Residual Plot

• 设有N个数据点{$x_i,y_i$}，拟合函数为$y=f(x)$。
• $x_i$点的残差(Residual)定义为$\Delta_i=y_i-f(x_i)$, $\Delta-x$二维图称为残差图(Residual plot)

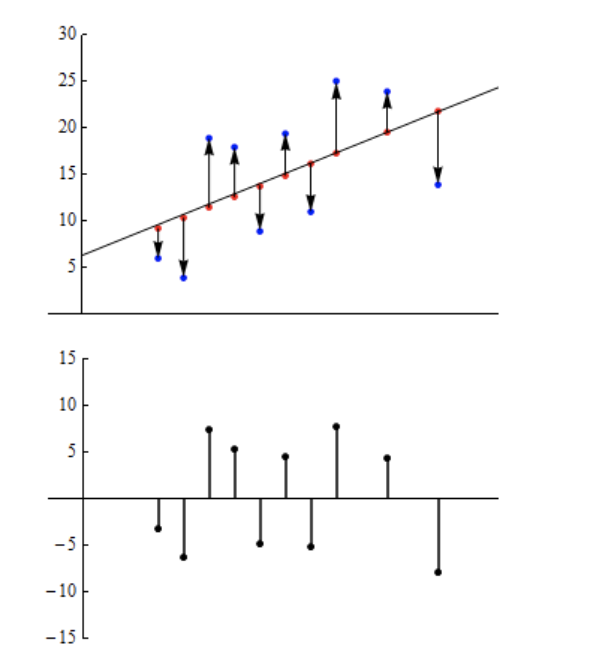
下图显示了10 个数据点的散点图和拟合曲线。

• 蓝点代表原始数据。为红点为拟合曲线给出的预测值。从预测值到数据点的垂直箭头代表残差。向上箭头对应于正残差，向下箭头对应于负残差。

• 在残差图中，每个值大于零的点对应于原始数据集中观测值大于预测值的数据点。类似地，负值对应于观测值小于预测值的数据点。 我们使用残差图来确定拟合函数的形式(模型)是否与数据分布一致。

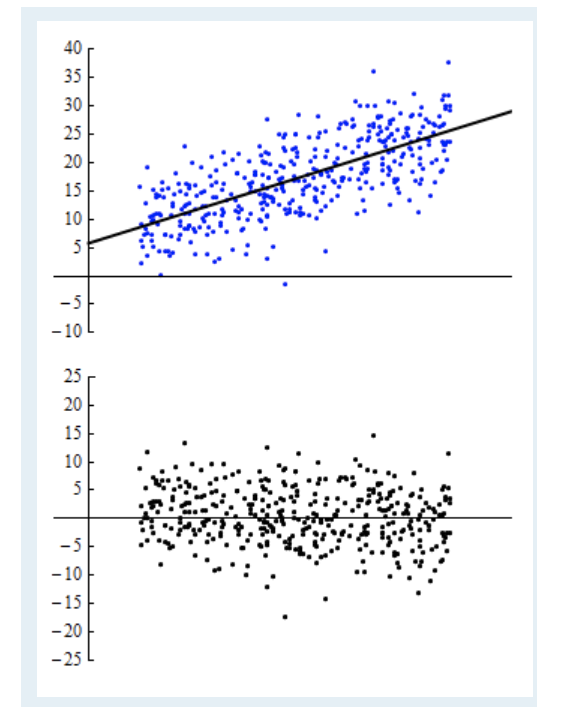
数据与模型一致

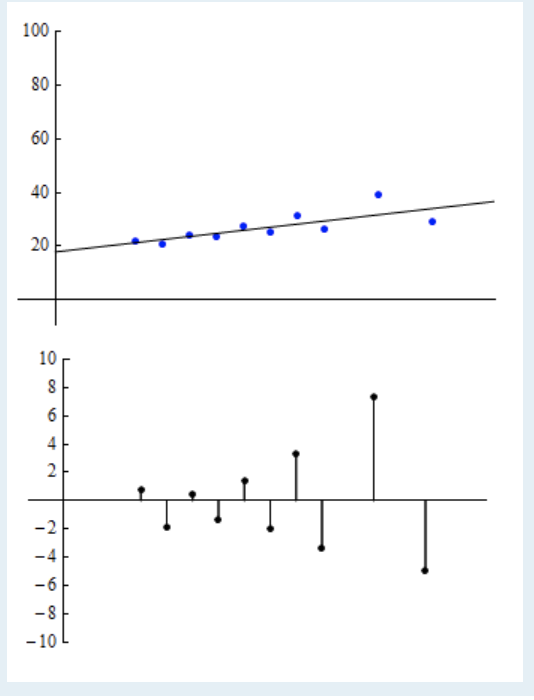
下图的数据，采用线性模型进行拟合。观察残差图可以发现，残差点是随机分散的。当我们从左到右检查残差时，沿x轴的方向残差的分散没有以任何系统的方式变宽或变窄。我们没有看到特定的模式。这说明了数据符合模型(即数据分布满足线性模型)。

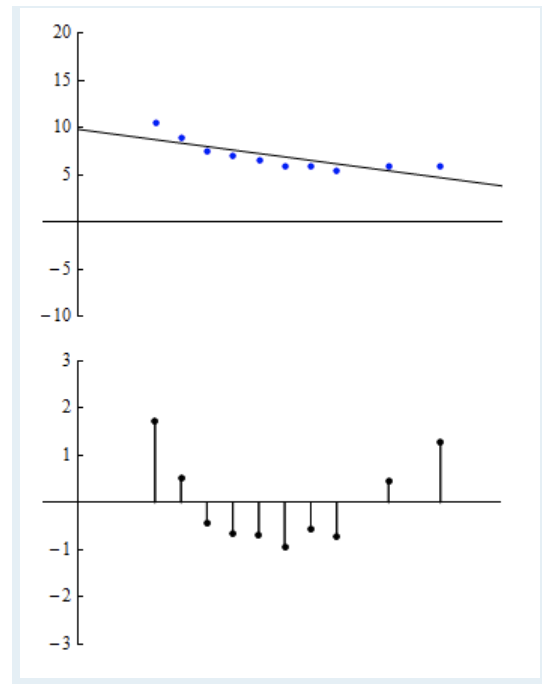
数据与模型不一致

1 残差分布显示特定的结构

• 粗略地看，散点图似乎显示出很强的线性关系。然而，当我们检查残差图时，我们会看到一个清晰的 U 形图案。散点图中数据点在回归线上方、下方和上方的移动是显而易见的。 残差图有助于我们关注数据与模型的偏差。

• 残差图中的模式表明线性模型可能不合适，因为模型预测对于解释变量范围中间的值来说太高，而对于该范围两端的值来说太低。在直线的基础上加入二次多项式的模型可能更合适。

残差的绝对值呈现特定的模式

例1.

• 残差的绝对值从左向右移动而稳步增大。换句话说，当我们从左向右移动时，观测值与预测值的偏差越来越大。

• 残差图中的模式表明单一的模型不能很好的描述数据。

  • 可能的方案是把数据点分成两组，分别用不同的模型描述。

例2.

• 残差在左侧和右侧比在中间更分散。
• 表明线性模型只能描述特定范围的数据。