HPGe 探测器 gamma 刻度方法¶
能量刻度¶
HPGe 探测器的能量刻度在相关能量范围(50keV - 3000 keV)内进行,使用经认证的标准源,即 $^{133}Ba$、$^{137}Cs$、$^{60}Co$、$^{152}Eu$、$^{22}Na$等,其能量以及绝对γ 射线发射概率已精确标定。此外,还可以考虑天然放射性核素 $^{40}K$ 和 $^{208}Tl$ 的能量线分别为 1460 keV 和 2614 keV。
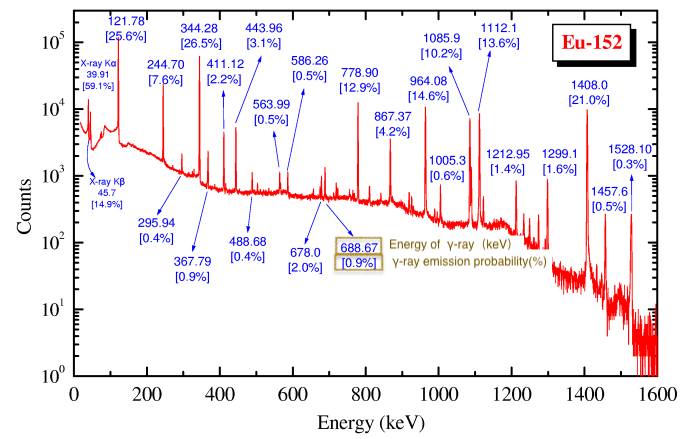
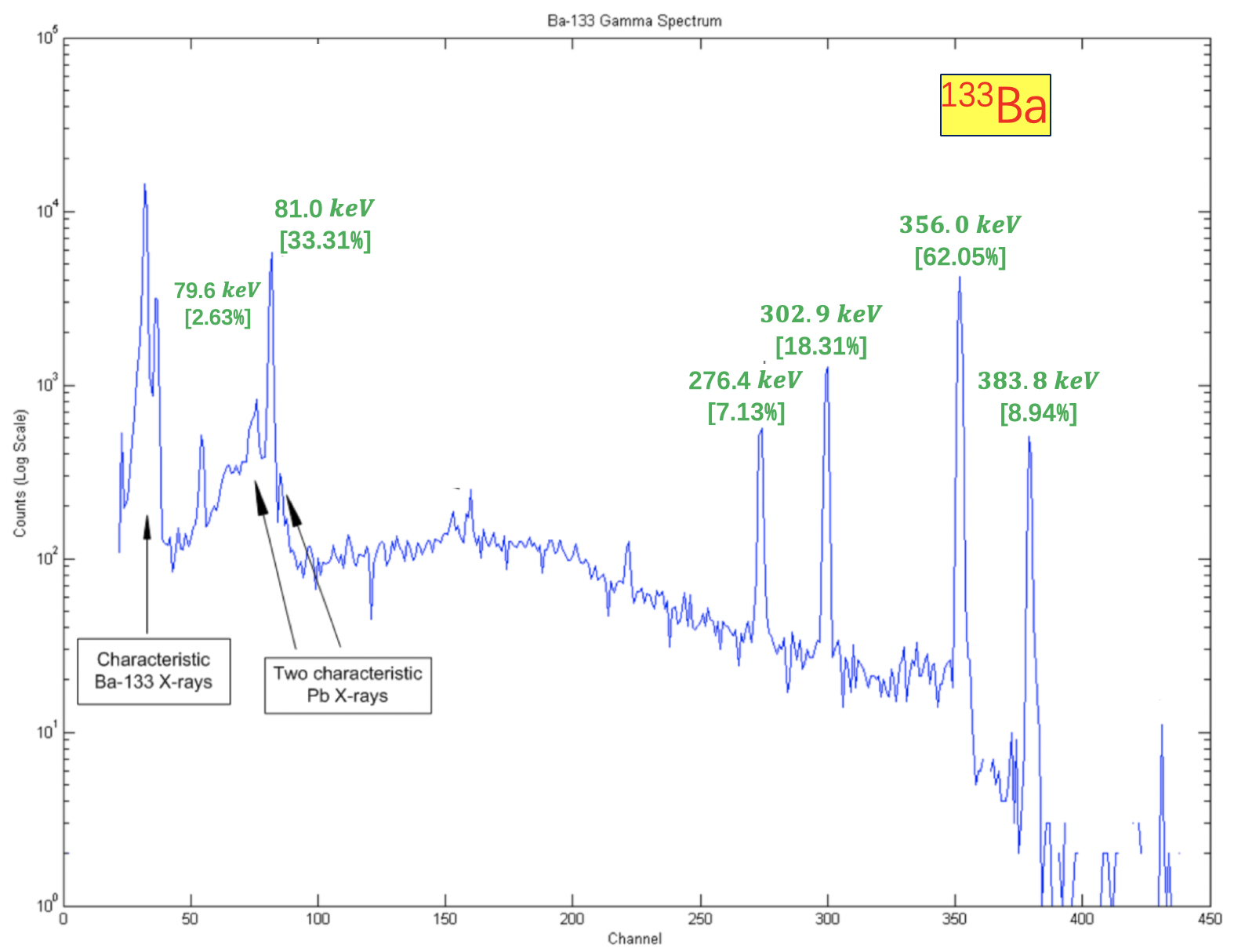
能量刻度曲线,由以下二次多项式函数描述:
$$Energy [keV] = a_0 +a_1 \times Channel + a_2 \times (Channel)^2$$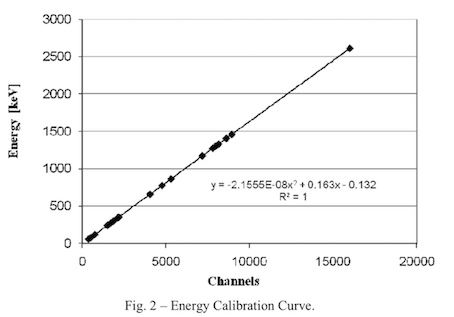
峰宽刻度¶
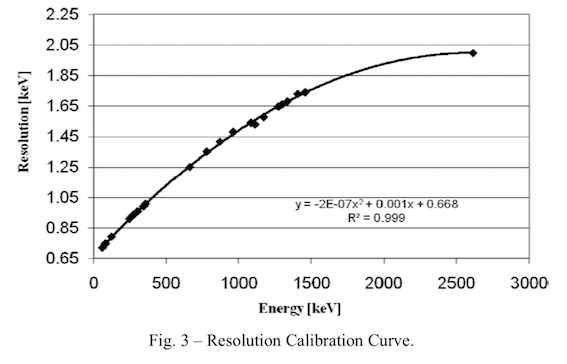
分辨率(FWHM)刻度曲线用二次多项式函数描述,如下所示:
$$FWHM [keV] = a_0 +a_1×E_{\gamma} + a_2×E_{\gamma}^2$$
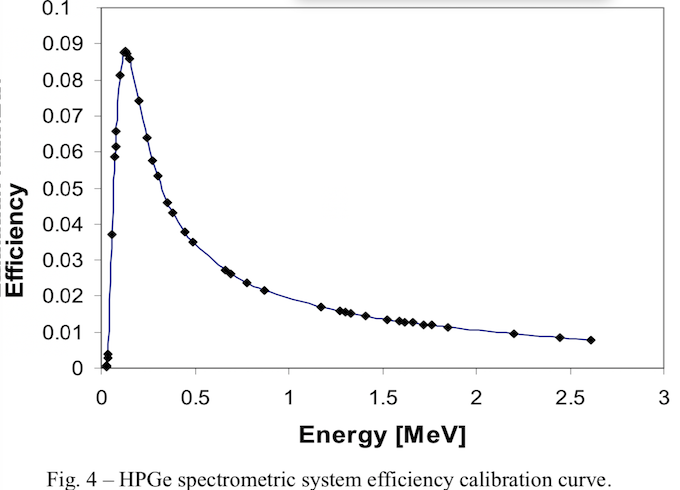
峰效率刻度¶
效率刻度使用上述标准源进行。能量 E 下的全能量峰值效率 ε(E) 可通过以下等式确定:
$$\varepsilon(E_{\gamma})=\frac{N(E_{\gamma})}{A_0e^{-\lambda t} P_{\gamma}\Delta t}$$式中,$N(E_{\gamma})$ 是计数的净面积,$A_0$ 源在出厂时标定的活度,$p_γ$ 是绝对γ 射线发射概率,$t$ 是出厂到当前的时间,λ 是衰变常数,$\Delta t$是测量时间。
峰值下的本底被定义为在一个区域内的平均计数,该区域等于$3 \Gamma$(3 FWHM),在峰值两侧延伸 $1.5 \Gamma$。净峰面积由下式得出
$$N=G-B_L-B_R$$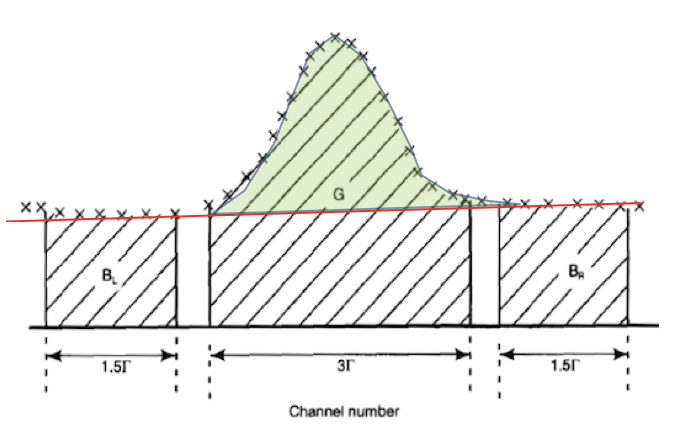
各种函数和函数组合可以用来描述效率的能量依赖性。例如,
$$\varepsilon(E)=1/E \sum_{i=1}^n a_i(ln E)^{i-1} \quad ,i=1-8(i\neq 5,7)$$
In [1]:
!jupyter nbconvert HpGe_Calibration_method.ipynb --to html