LISE++ energy loss calculation¶

  • LISE++ 是计算放射性束流线中次级带电粒子碎片生成、传输的工具包，内部还集成了很多核物理实验和计算中用到的计算程序。
  • LISE++ 安装 下载链接 for Windows/linux/Mac OS
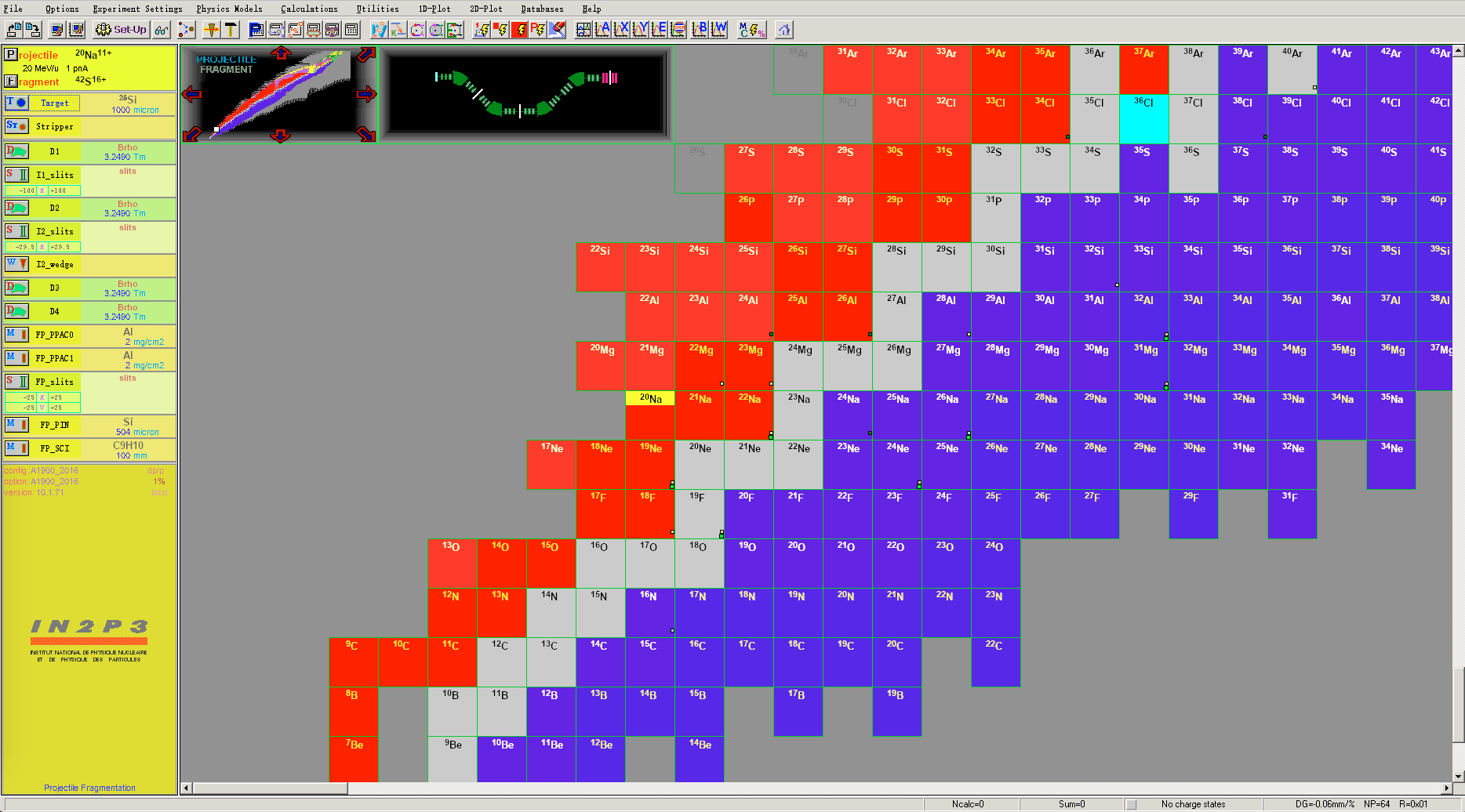
  • LISE++ 界面

Range/dE/dx¶

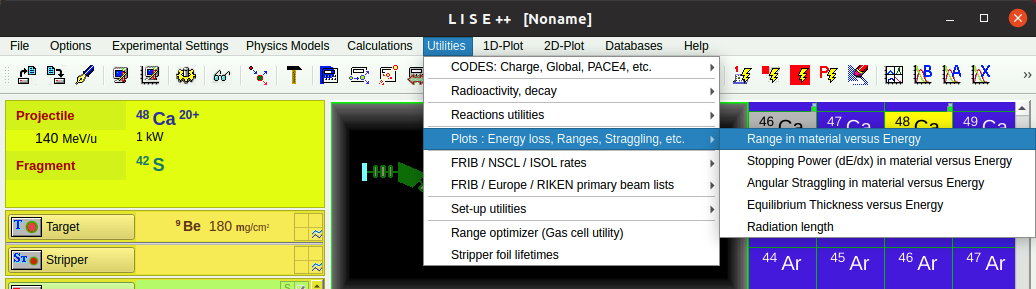
  • Lise Menu$\to$ Utilities $\to$ Plots: Energy loss, Ranges ...
  • 选择不同的选项卡可以得到能损曲线和射程曲线
    • $\to$ Stopping power(dE/dx) ...   dE/dx ~ e
    • $\to$ Range in material ...      Range ~ e

获得dE/dx~E 数据步骤：¶

  • 从菜单栏中进入Stopping power(dE/dx) ... 选项卡

  • 设定注入粒子(Projectile)和靶材料(Material)，单位选择micron(um).

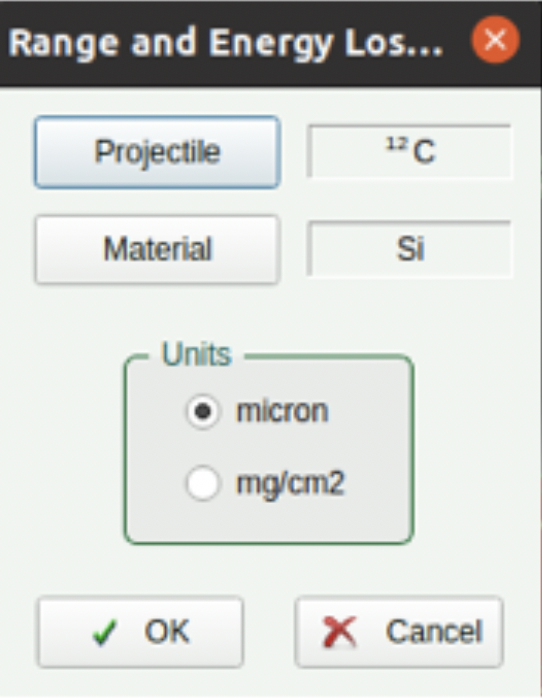
  • 靶材料选择界面：

    • 靶为单质

      • 选择同位素和状态(气态，固态)

    • 靶为化合物或混合物

      • 按照比例依次添加不同同位素

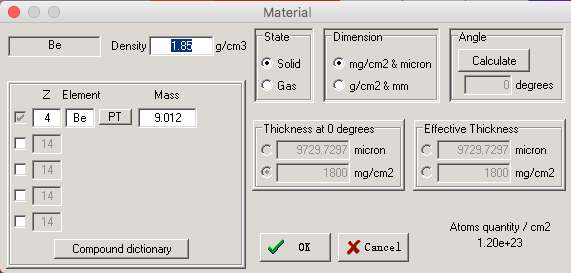
    • 选择给定化合物或混合物
      • 上图中选择左下方Compound dictionary.
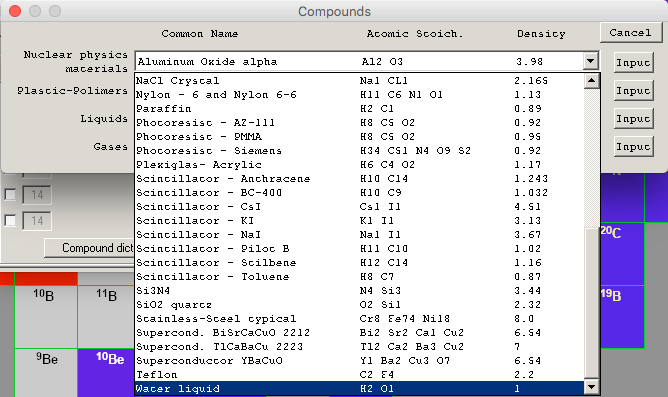
      • 将材料按照分类列在不同的种类中。
      • 选择下拉栏中合适材料,比如water liquid。
      • 点击右侧Input按钮，导入靶材料。

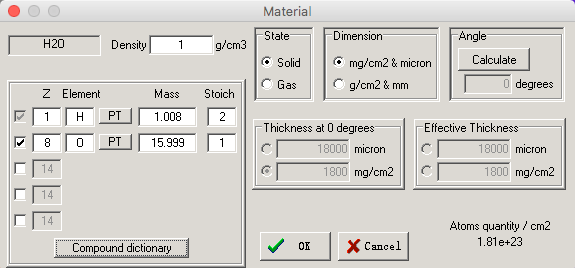
  • 点击 OK 即可获得能损曲线。在我们感兴趣的能量范围 1e-2 - 1e4 MeV/u，几条模型给出的曲线(下图中1-4)结果基本一致。

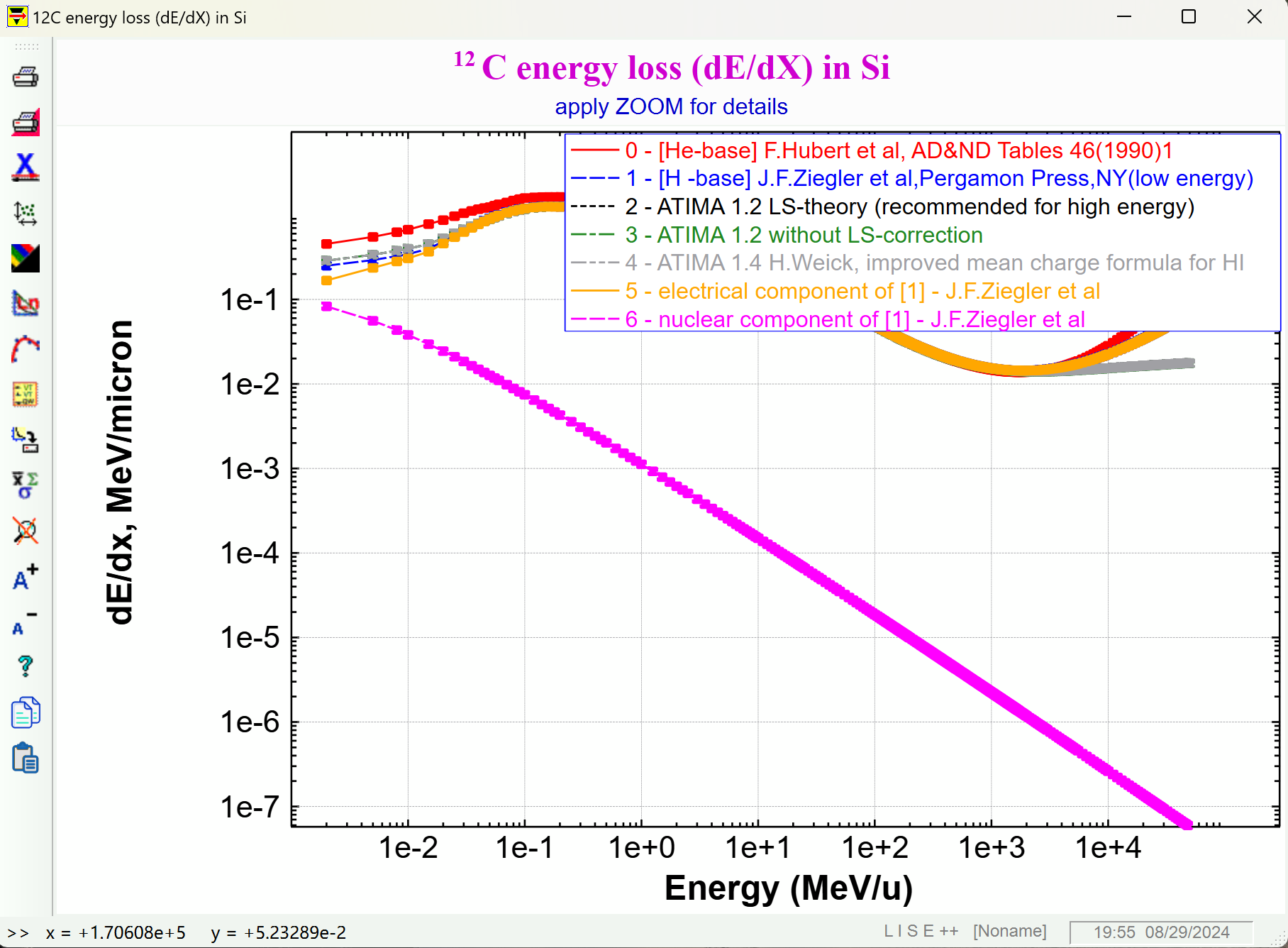
  • 按左侧边栏图标可以改变图形显示方式，点击 Save As 图标保存数据文件。
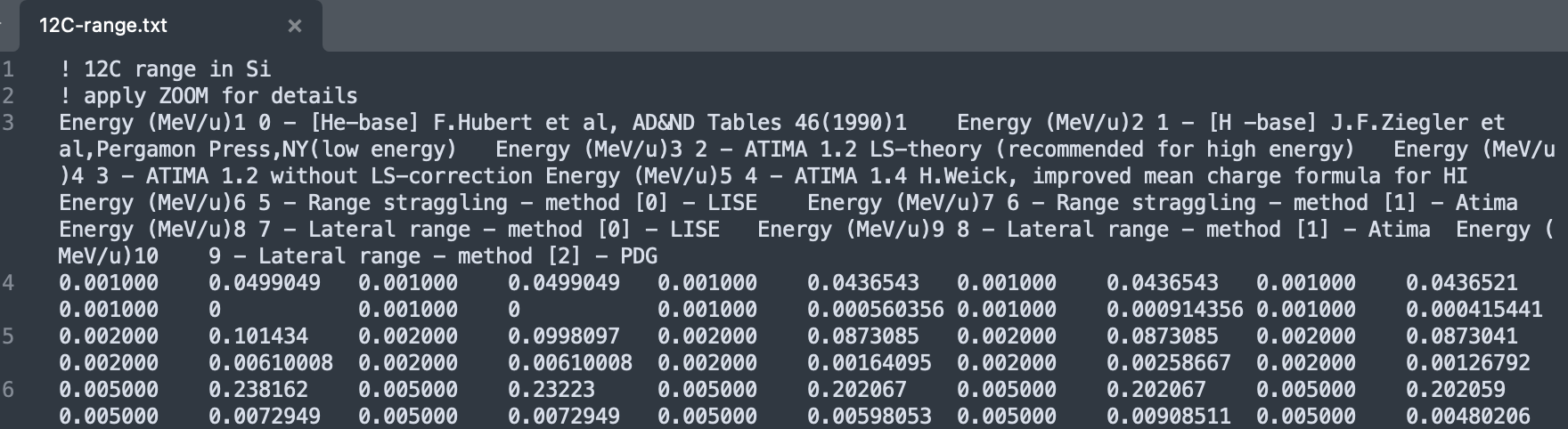
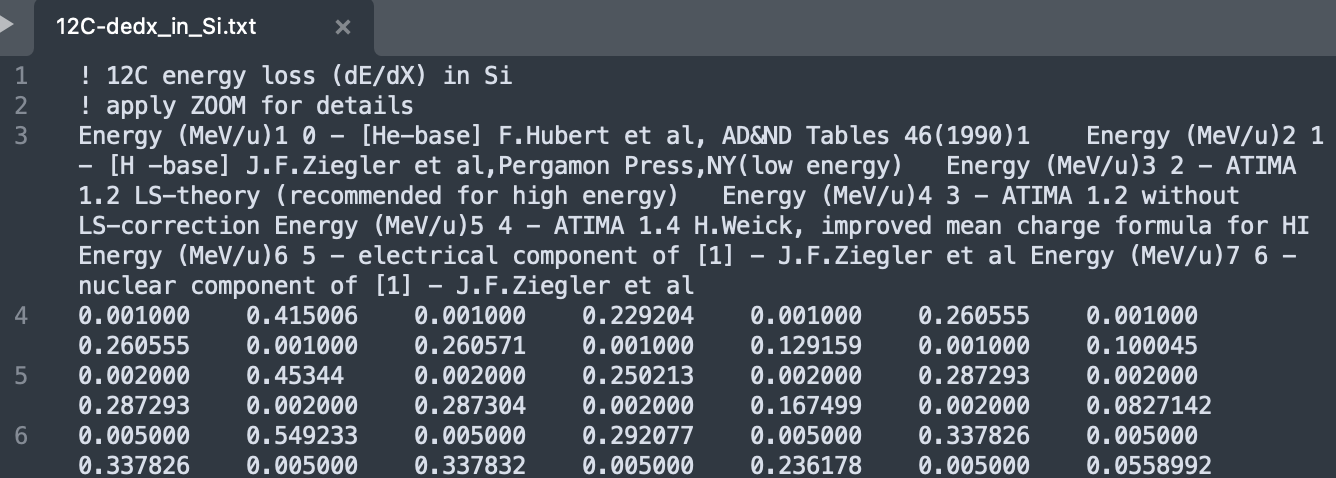
  • 最终获得数据文件如下：示例数据文件

获得Range~E 数据步骤：¶

  • 选择Range in material ... ...选项卡

  • 重复上述步骤

// 0 - [He-base] F.Hubert et al, AD&ND Tables 46(1990)1
  // 1 - [H -base] J.F.Ziegler et al,Pergamon Press,NY(low energy)
  // 2 - ATIMA 1.2 LS-theory (recommended for high energy)
  // 3 - ATIMA 1.2 without LS-correction
  // 4 - ATIMA 1.4 H.Weick, improved mean charge formula for HI ----
  // 5 - Range straggling - method [0] - LISE
  // 6 - Range straggling - method [1] - Atima
  // 7 - Lateral range - method [0] - LISE
  // 8 - Lateral range - method [1] - Atima
  // 9 - Lateral range - method [2] - PDG
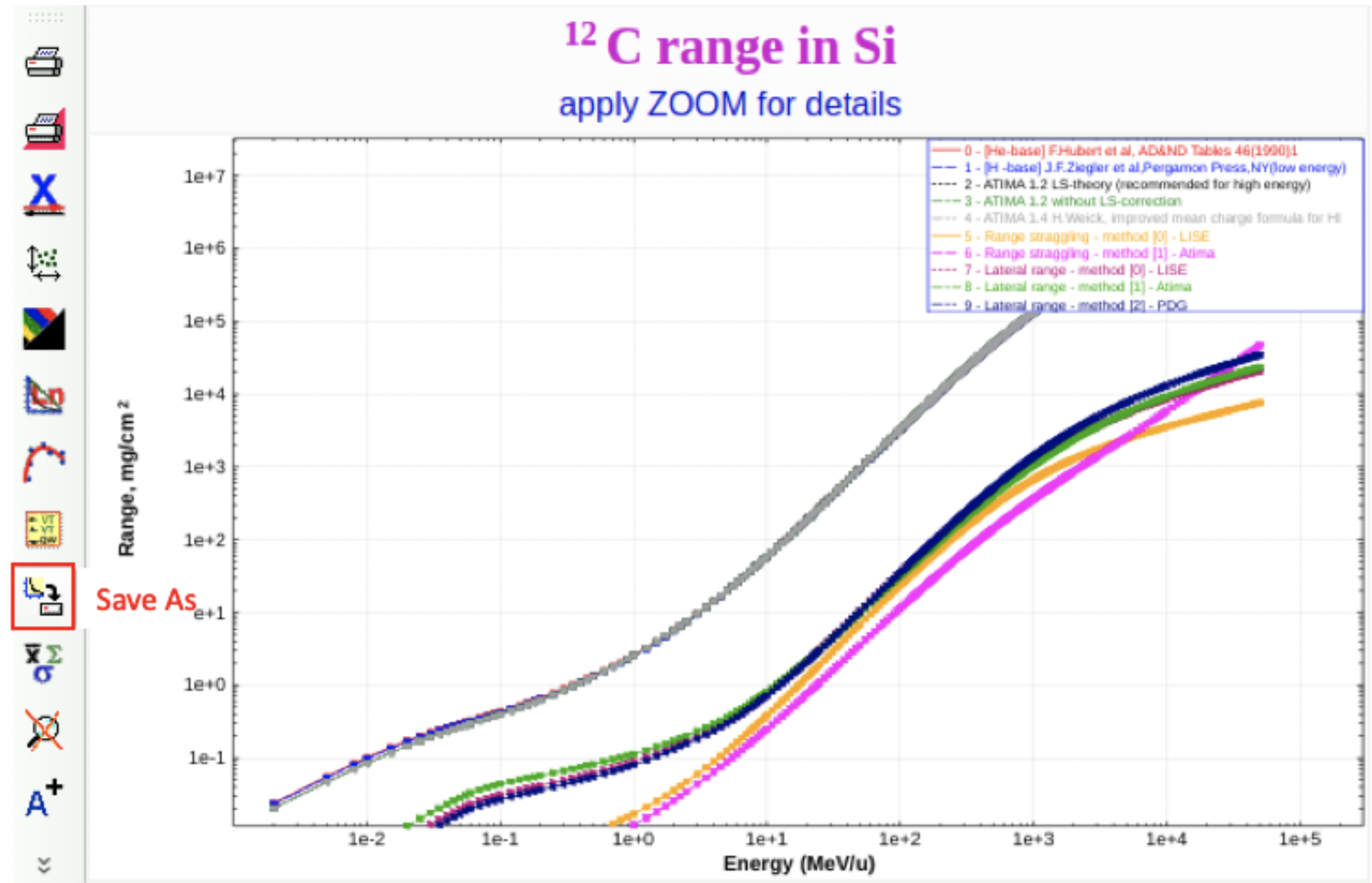
  • 最终获得数据文件如下：示例数据文件

Read dE/dx data into a TGraph¶

  • energy: MeV/u, dE/dx: MeV/$\mu m$
In [1]:
TCanvas *c1 = new TCanvas;
In [2]:
TGraph *gEdEdxLISE(const char* inputFile)
{
  ifstream inFile(inputFile);
  if (!(inFile.is_open())) {                                                        
    cout << "Cannot find input file :" <<inputFile << endl;
    return 0;
  }   
  TGraph *gEdEdx = new TGraph;
  string str;
  for(int i=0;i<3;i++) 
    getline(inFile, str); // skip the first three lines

  // energy: MeV/u, Range: micron - do not depends on A.

  double energy, R[10], dummy;
  int n=0;
  while (getline(inFile,str) ) 
    {
        stringstream ss(str);
        ss  >> energy >> R[0] 
            >> dummy  >> R[1]
            >> dummy  >> R[2] 
            >> dummy  >> R[3] 
            >> dummy  >> R[4]  /* used for calculation */
            >> dummy  >> R[5]; 

        gEdEdx->SetPoint(n++, energy, R[4]);
    }
  inFile.close();
  cout << "Read " << n << " lines of data from the file: " << inputFile << endl;
  cout << "TGraph: x = E(MeV/u), y = dEdx(MeV/um) " << endl;
  return gEdEdx;
}
In [3]:
TGraph *gEdEdx = gEdEdxLISE("12C-dedx_in_Si.txt");

Read 268 lines of data from the file: 12C-dedx_in_Si.txt
TGraph: x = E(MeV/u), y = dEdx(MeV/um)

12C在Si中的能损曲线¶

In [4]:
{
    gEdEdx->SetTitle("gEdEdx: dE/dx(MeV/um) vs Energy(MeV/u); MeV/u; MeV/um");
    gEdEdx->SetLineColor(kBlue);
    gEdEdx->SetMarkerColorAlpha(kRed,0.2);
    gEdEdx->Draw("AL*");
    c1->SetLogy();
    c1->SetLogx();
    c1->Draw();
}

计算给定能量的12C在Si中的能损.¶

In [5]:
cout<< "dE/dx of 120 MeV(=10 MeV/u) 12C in a Silicon detector: " << gEdEdx->Eval(120./12,0,"S") << " MeV/um" << endl;

dE/dx of 120 MeV(=10 MeV/u) 12C in a Silicon detector: 0.294849 MeV/um
In [ ]:

Read Range data into a TGraph¶

  • energy: MeV/u, Range: $\mu m$
In [6]:
TGraph *gERangeLISE(const char* inputFile)
{
  ifstream inFile(inputFile);
  if (!(inFile.is_open())) {                                                        
    cout << "Cannot find input file :" <<inputFile << endl;
    return 0;
  }   
  TGraph *gER = new TGraph;
  string str;
  for(int i=0;i<3;i++) 
    getline(inFile, str); // skip the first three lines

  // energy: MeV/u, Range: micron - do not depends on A.

  double energy, R[10], dummy;
  int n=0;
  while (getline(inFile,str) ) 
    {
        stringstream ss(str);
        ss  >> energy >> R[0] 
            >> dummy  >> R[1]
            >> dummy  >> R[2] 
            >> dummy  >> R[3] 
            >> dummy  >> R[4]  /* used for calculation */
            >> dummy  >> R[5] 
            >> dummy  >> R[6] 
            >> dummy  >> R[7] 
            >> dummy  >> R[8] 
            >> dummy  >> R[9];
        gER->SetPoint(n++, energy, R[4]);
    }
  inFile.close();
  cout << "Read " << n << " lines of data from the file: " << inputFile << endl;
  cout << "TGraph: x = E(MeV/u), y = Range(um) " << endl;
  return gER;
}
In [7]:
TGraph *gER = gERangeLISE("12C-range_in_Si.txt");

Read 268 lines of data from the file: 12C-range_in_Si.txt
TGraph: x = E(MeV/u), y = Range(um)

12C在Si中的射程曲线¶

In [8]:
{
    gER->SetTitle("gER: Range(um) vs Energy(MeV/u); MeV/u; um");
    gER->SetLineColor(kBlue);
    gER->SetMarkerColorAlpha(kRed,0.2);
    gER->Draw("AL*");
    c1->SetLogy();
    c1->SetLogx();
    c1->Draw();
}

计算给定能量的粒子在Si中的射程.¶

In [9]:
cout<< "Range of 120 MeV(=10 MeV/u) 12C in a Silicon detector: " << gER->Eval(120./12,0,"S") << " um" << endl;

Range of 120 MeV(=10 MeV/u) 12C in a Silicon detector: 249.686 um

利用射程曲线, 计算能量为$E_0$的C粒子在厚度为$\Delta x$的Si上的能量损失¶

  • 计算入射能量为$E_0$的入射粒子在Si中的射程 $R(E_0)$ = gER->Eval($E_0$)

  • $R_1 = R(E_0)-\Delta x$ 为能量为$E_0$的粒子经过$\Delta x$后剩余的射程。

  • 从 $R(E)$ 中可推出 $E(R)=R^{-1}(E)$。 射程为 $R_1$ 的粒子对应的入射能量为 $E_1=E(R_1)$ 。

  • 由下面公式可以计算$\Delta E$:

$$ R_1 = R(E_0)-\Delta x\\ E_1 = E(R_1)\\ \Delta E = E_0 - E_1 $$
In [10]:
void draw(double x0, double y0, double x1, double y1, double tx0, double ty0, TString txt)
{
    TArrow *arrow = new TArrow(x0, y0, x1, y1, 0.005);
    TLatex *tex = new TLatex(tx0,ty0,txt);
    
    arrow->SetLineColor(kBlue);
    arrow->SetLineStyle(2);
    arrow->Draw();

    tex->SetTextFont(13);
    tex->SetTextSize(15);
    tex->SetTextAlign(12);
    tex->SetTextAngle(0);
    tex->SetTextColor(kRed);
    tex->Draw();
}
In [11]:
{
    gER->SetTitle("gER: Range(um) vs Energy(MeV/u); MeV/u;um");
    gER->SetLineColor(kBlue);
    gER->SetMarkerColorAlpha(kRed,0.2);
    gER->Draw("AL*");
    draw(40,0,40,gER->Eval(40),40,0.01,"E_{0}");
    draw(20,0,20,gER->Eval(20),20,0.01,"E_{1}");
    draw(0,gER->Eval(40),40,gER->Eval(40),1.0e-4,gER->Eval(40),"R(E_{0} )");
    draw(0,gER->Eval(20),20,gER->Eval(20),1.0e-4,gER->Eval(20),"R(E_{1} )");
    c1->SetLogy();
    c1->SetLogx();
    c1->Draw();
}

如何得到E(R)：

  • TGraph $*$g： 无法直接从 y=f(x)=g->Eval(x)，得到反函数 x = f$^{-1}$(y)

  • 将TGraph* gER 的 x 和 y 交换, 生成 TGraph* gRE:

TGraph *gRE = new TGraph(gER->GetN(),gER->GetY(),gER->GetX());//swap E and R: E(R)
  • $R_1$ 对应的入射能量为 $E_1$ = gRE->Eval($R_1$).
In [12]:
{
    TGraph * gRE = new TGraph(gER->GetN(),gER->GetY(),gER->GetX());    
    gRE->SetTitle("gRE: Energy(MeV/u) vs Range(um); um; MeV/u");
    gRE->SetLineColor(kBlue);
    gRE->SetMarkerColorAlpha(kRed,0.2);
    gRE->Draw("AL*");

    draw(1e3,0,1e3,gRE->Eval(1e3),1e3,0.2e-3,"R_{1}");

    draw(0,gRE->Eval(1e3),1e3,gRE->Eval(1e3),0.8e-2,gRE->Eval(1e3),"E(R_{1} )");

    c1->SetLogy();
    c1->SetLogx();
    c1->Draw();
}

200 MeV的$^{12}$C粒子在 300$\mu m$ Si中的能损¶

In [13]:
{
    
    TGraph * gRE = new TGraph(gER->GetN(),gER->GetY(),gER->GetX());
    
    int A = 12;
    double dx = 300; // um
    double E0_A = 200./12; // MeV
    double E0 = E0_A * A; //MeV
    double dE;
    double RE0 = gER->Eval(E0/A,0,"S");

    if(RE0 > dx) {
        double RE1 = RE0 - dx;
        double E1 = gRE->Eval(RE1,0,"S");
        dE = E0 - E1*A;
    }
    else
        dE = E0;
    cout << "Energy loss of " << E0 << " MeV 12C in "
         << dx <<" um Silicon: " << dE << endl;

}

Energy loss of 200 MeV 12C in 300 um Silicon: 69.3239

可将上述功能封装成函数¶

double eloss(int A, double E0_A, double dx, TGraph *gER, TGraph *gRE)
{
/* ... */
}
cout<< eloss(12, 200./12, 300, gER)<<endl;

69.3239