HPGe calibration - tutorial¶
1.从文件中读取能谱¶
//%jsroot on
TCanvas *c1 = new TCanvas("c1");
// 从文件中读取能谱
TFile *filer = new TFile("gamma.root","READ");// 以只读模式打开ROOT文件
if(!filer->IsOpen())
{
std::cout<<"Can't open root file"<<std::endl;
}
TH1F *h_gammaraw = (TH1F*)filer->Get("h0");//通过指针读取原始gamma谱
// 通过指针 h_gammaraw 可对直方图进行操作
h_gammaraw->Draw();
c1->Draw();
- 开启 jsroot on,可以操作图像对数坐标显示。也可以拖动局部显示图像。
- 将鼠标放置在图像左下角的实心方块上,会显示很多小按钮。探索一下每个按钮的功能
上图为未刻度的gamma谱,其中横轴为道址,纵轴为计数。进行刻度时参照刻度方法中给出的$^{152}Eu$和$^{133}Ba$能谱,查找到对应峰位进行刻度。
2.最小二乘法拟合¶
Gauss 拟合¶
- 拟合能量峰位的时候可以采用Gauss拟合。
下图是Gauss拟合中返回的拟合参数的一个示例。 其中constant、mean、sigma,的Values 分别代表着高斯函数的高度、峰位、和展宽的拟合值。上述每项对应的Error为该项的拟合误差。
- 峰位的拟合误差应选用mean对应的Error值,而非sigma值。
// 对某个峰进行高斯拟合
h_gammaraw->Fit("gaus","","",1215,1219);// 这里 1215 为拟合的左边界,1219 为拟合的右边界
h_gammaraw->Draw();
h_gammaraw->GetXaxis()->SetRangeUser(1212,1222);//设置显示的区间
c1->Draw();
// 拟合需要选择合适的拟合区间。
// 由拟合输出信息可以获得峰位及误差信息。
// 这里需要注意,选取合适的拟合区间对于峰位的精确指认至关重要。评判拟合好坏的一个标准是拟合曲线与实际曲线越贴近越好。
h_gammaraw->GetXaxis()->SetRangeUser(0,2500);//返回全区间,在多次进行拟合时,必须要有这个操作,否则指定的拟合区间将存在问题
h_gammaraw->Fit("gaus","","",842,846);//指定拟合的左右边界, 在Fit函数的第二个参数设为"L"时进行最大似然法拟合
h_gammaraw->Draw();
h_gammaraw->GetXaxis()->SetRangeUser(840,848);//设置显示的区间
c1->Draw();
double fun(double *x, double *par)//高斯函数par[0-2]+线性函数par[3-4]
{
return par[0]*TMath::Exp(-0.5*((x[0]-par[1])/par[2]) * ((x[0]-par[1])/par[2])) + par[3]+x[0]*par[4];
}
拟合函数的参数初值设定+拟合¶
- 除了Gaus,poln(多项式)等简单拟合函数外,其他拟合函数一般要在拟合前给定合理的初值,才能正确收敛到正确的初值。如果初始值指定与实际值偏离很远,拟合结果有可能不收敛。
- 如对于下图的拟合:
- gauss函数初值中的par[0]-par[2]可设为仅用gauss函数拟合得到的constant,mean,sigma值
- 线性函数的b即par[3]可设为峰左右的平台平均高度,斜率k,即par[4]可设为比较小的值。
- 也可在峰左右的线性区域,进行线性拟合得到对应的par[3],par[4]的值。
TF1 *ffit = new TF1("ffit",fun,0,2500,5);// 0 跟 2500 为 左右边界, 5 表示总共有五个参数
ffit->SetParameter(0,1.0e6);//par[0]-高斯函数高度
ffit->SetParameter(1,332.0);//par[1]-高斯函数峰中心
ffit->SetParameter(2,1.0);//par[2]-高斯函数sigma
ffit->SetParameter(3,1.0e3);//par[3]-线性函数零次项
ffit->SetParameter(4,0.01);//par[4]-线性函数一次项
h_gammaraw->GetXaxis()->SetRangeUser(0,2500);//返回全区间
h_gammaraw->Fit("ffit","","",328,338);
h_gammaraw->Draw();
h_gammaraw->GetXaxis()->SetRangeUser(325,340);//X轴的显示范围
c1->Draw();
将数据填入 TGraphErrors 进行拟合¶
第一章的作业中用到的 TGraph,一般用来表达没有误差的二维数据点的分布。当数据有误差时需要用 TGraphErrors,如以上拟合得到的峰位值有误差值。
仿照下面链接 TGraphErrors Class Reference 的做法,将数据(包含误差值)填入TGraphErrors,并画图。$^{152}Eu$,$^{133}Ba$ 的能量值 [keV] 的误差全部设置为0。
关于 TGraphErrors 的使用,也可参考 jupyter 上 ROOT Tutorial/TGraph.ipynb 文件中关于 TGraphErrors 的实例。实例中包含了如何进行数据点的拟合。
关于ROOT fit的更详细用法参考以下链接 FittingHistograms
应用获得的刻度系数绘制 𝛾 能谱¶
在获得能量刻度系数之后,应用刻度系数即可获得刻度后的能谱。然而直接对直方图进行变换会出现一些并道的问题,这里不做过多阐述。简化起见,提供如下示例代码,供大家应用刻度系数直接生成刻度后的能谱。
double p0 = 0;//填入拟合得到的数值
double p1 = 1;
double p2 = 0;
TH1D *h1 = new TH1D("h1","",10000,0,2500);//h1为刻度后的gamma谱
TRandom3 *r = new TRandom3(0);
int Nbins = h0->GetXaxis()->GetNbins(); //h0为未刻度的gamma谱。
for(int i=0; i<Nbins; i++)
{
Long64_t eN = h0->GetBinContent(i);// GetBinContent()提取每个bin的计数
Double_t e = h0->GetBinLowEdge(i);// GetBinLowEdge()提取每个bin左边界的横坐标x。
for(Long64_t j=0; j<eN; j++)
{
Double_t ea = e+r->Rndm()*0.2;// 思考下为何要加上一个随机数??????????????
ea=p2*ea*ea+p1*ea+p0;//p0,p1,p2为上面获得的二次项刻度系数。
h1->Fill(ea);
}
}
h1->Draw();
c1->Draw();
刻度好的$\gamma$峰的能量值应与下图标示数值接近。

3. 计算gamma峰面积(峰计数)¶
计算峰面积采用HPGe gamma 探测器刻度方法中给出的面积求法。应用高斯加线性拟合获得的sigma参数,选取mean-1.5sigma,mean+1.5sigma范围,进行积分。获得峰位总计数S1。
在峰附近左右两侧各选择1.5*sigma范围进行积分,获得S2,S3,用于估计峰的本底。
从而可以获得质子峰计数S=S1-S2-S3.
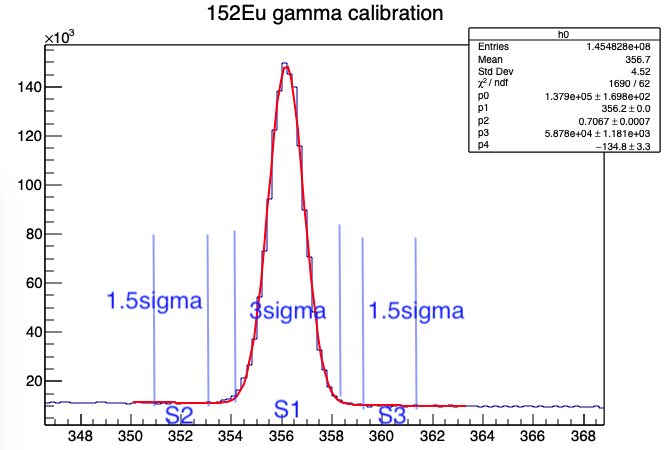
如何从直方图中提取面积
如下图,若要获得红线区域内面积,需要提取出拟合范围左右边界的binx项。
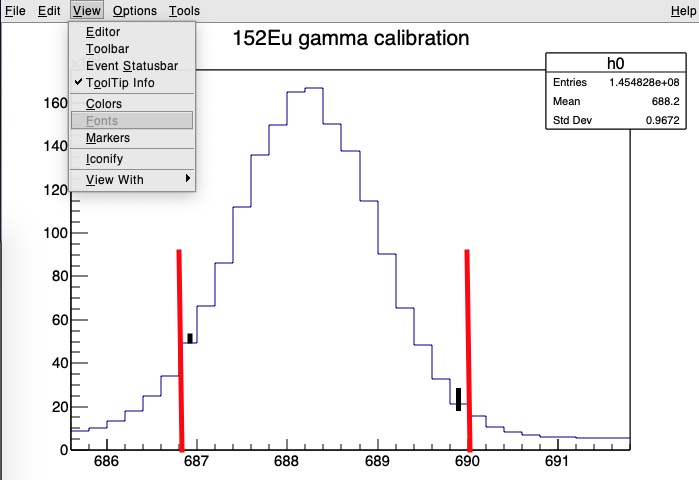
int bin1=h0->FindBin(686.9);//686.9为积分左边界,对应bin值3435
int bin2=h0->FindBin(689.9);//689.9为积分右边界,对应bin值3450
h0->Integral(bin1,bin2);//计算区域总计数
即可获得区域内总计数。