Invariant Mass¶
Invariant mass is a Lorentz-invariant quantity that characterizes the total energy and momentum of a particle or system, remaining constant across all reference frames. It’s a cornerstone for analyzing particle collisions and decays.
The invariant mass for two particles with four-momenta $ P_1 = (E_1, \vec{p}_1) $ and $ P_2 = (E_2, \vec{p}_2) $ is defined as:
$$ M^2_{Inv} = (P_1 + P_2)^2 = (E_1 + E_2)^2 - |\vec{p}_1 + \vec{p}_2|^2 $$Here, $ E_i $ is the energy, $ \vec{p}_i $ is the three-momentum, and units assume $ c = 1 $. For a system of $ n $ particles, this generalizes to:
$$ M(n)^2_{Inv} = (P_1 + P_2 + \dots + P_n)^2 $$For a single particle, the invariant mass equals its rest mass, $ m_0 $, since in its rest frame, $ P = (m_0, 0, 0, 0) $, yielding:
$$ M^2_{Inv} = m_0^2 $$This invariance makes it ideal for identifying particles or resonances, regardless of the observer’s frame.
Intermediate States and Resonances¶
In collision experiments, short-lived intermediate particles or resonances often decay into secondary particles. To confirm their existence, physicists measure the four-momenta of decay products and compute the invariant mass of specific combinations. A peak in the invariant mass distribution indicates a resonance. For example, in $ Z \to e^+ + e^- $, the invariant mass of the electron-positron pair peaks around 91 GeV, confirming the Z boson.
Two-Body Collision Reactions¶
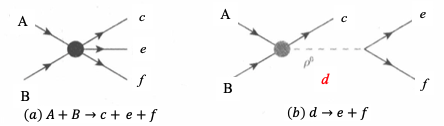
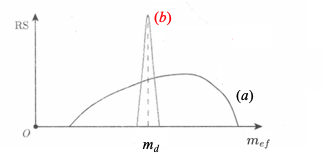
Consider a reaction $ A + B \to \text{products} $. Two processes highlight distinct invariant mass behaviors:
Process (a): $ A + B \to c + d + e $
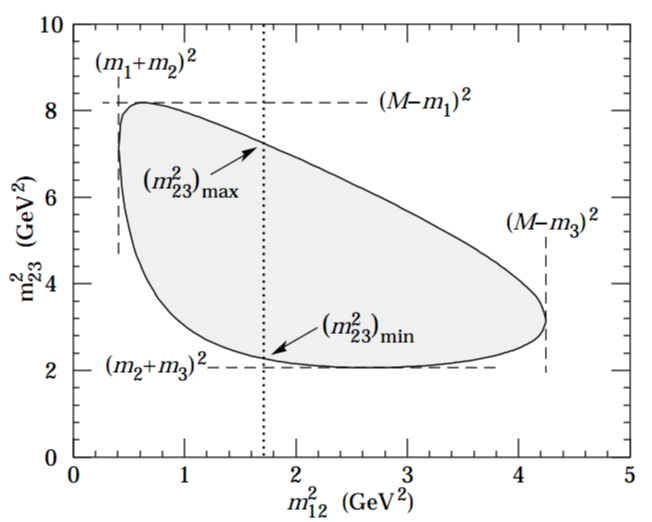
$$ M^2_{c+d} \sim \text{phase space distribution} $$
This is a 2 → 3 scattering process, producing three particles directly. The invariant mass of a pair, e.g., $ c + d $, follows a statistical distribution governed by phase space, which defines kinematic constraints (energy-momentum conservation). This results in a broad, continuous spectrum:Process (b): $ A + B \to c + d, d \to e + f $
$$ M^2_{e+f} \sim \text{Breit-Wigner}(m_d, \Gamma_d) $$
Here, $ c $ and an intermediate particle $ d $ are produced, with $ d $ decaying into $ e + f $. The invariant mass of $ e + f $ follows a Breit-Wigner distribution, centered around the mass of $ d $, with a width determined by its lifetime:For example, if $ d $ is a rho meson ($ \rho \to \pi^+ + \pi^- $), the pion pair’s invariant mass distribution peaks around 770 MeV with a Breit-Wigner shape.
Missing Mass¶
Missing mass complements invariant mass in experiments where particles (e.g., neutrinos) escape detection. By measuring the four-momenta of detected particles and knowing the initial state (e.g., $ P_A + P_B $), the missing four-momentum $ P_{\text{miss}} $ is calculated as:
$$ P_{\text{miss}} = (P_A + P_B) - (P_{\text{detected}}) $$The invariant mass squared of this missing four-momentum gives the missing mass:
$$ M^2_{\text{miss}} = P_{\text{miss}}^2 $$This quantity reveals properties of undetected particles, such as their mass, and is consistent with the total invariant mass of the system.
Example: Detecting Short-Lived Resonances¶
Particles liken $\rho,\omega,\phi$ have an average lifetime of 10$^{-22}$-10$^{-23}$s
- How do we know of their existence if they live so shortly?
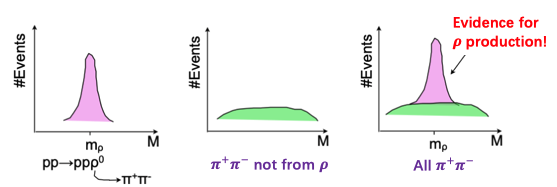
reaction pp$\to$ pp$\pi^+\pi^-$
- We identify all four particles in the final state and measure their momentum
- Let's focus on the pion pair, the total energy & momentum are: $E=E_{\pi^+}+E_{\pi^-} \space\space\space\space P=P_{\pi^+}+P_{\pi^-}$
- The invariant mass is: $M=(E^2- P^2)^{1/2}$
- The event distribution for the variable M from $\pi^+\pi^-$ will look like