Simulation¶
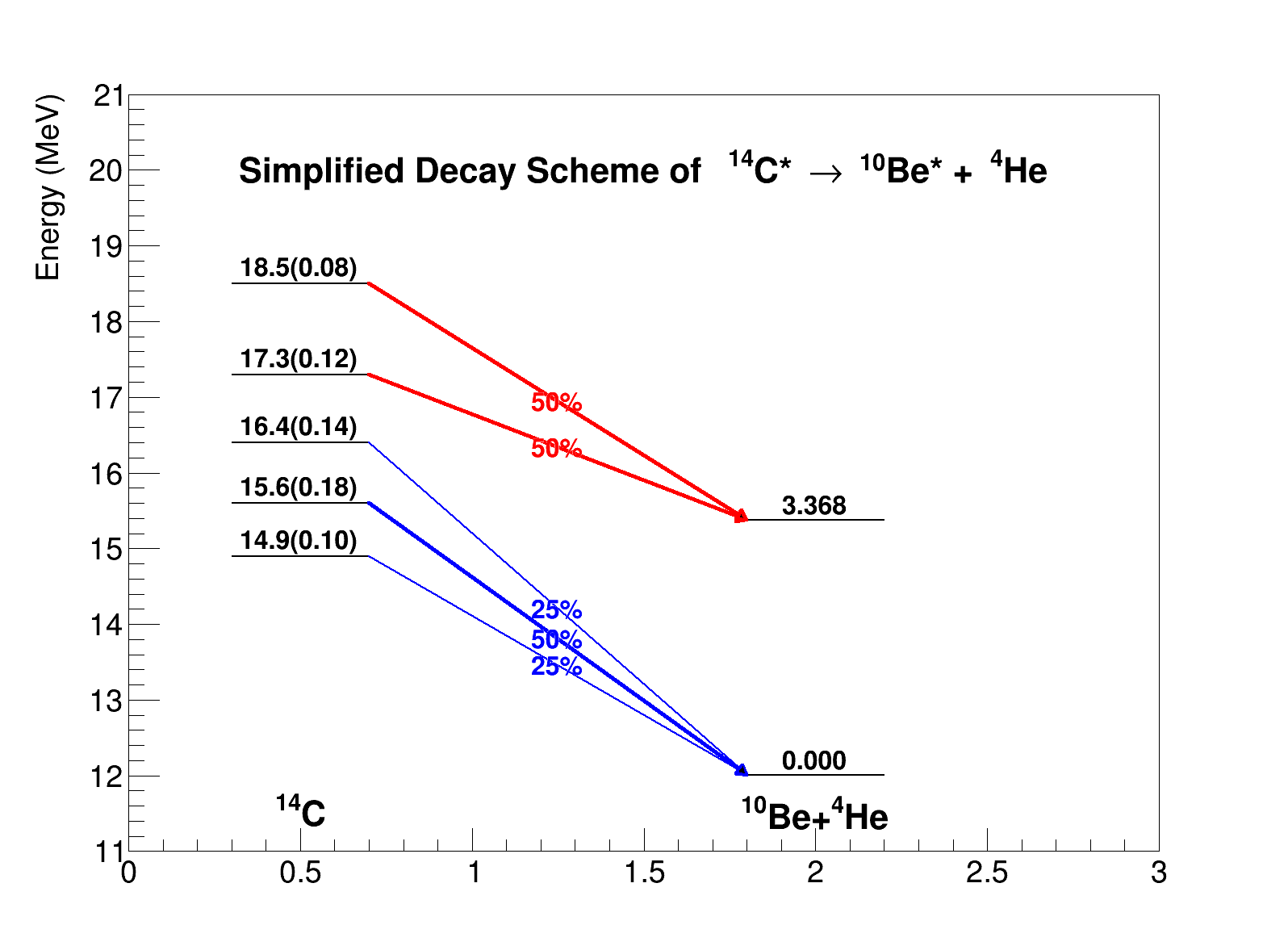
Model a two-step nuclear reaction where a $^{14}\text{C}$ beam interacts with a $^1\text{H}$ target, forming a compound system that decays into $^1\text{H}$ and an excited $^{14}\text{C}^*$, which further decays into $^4\text{He}$ and an excited $^{10}\text{Be}^*$ . It generates events by sampling excitation energies, simulating phase-space decays, and applying experimental resolutions to compute kinematic observables like energies and angles, storing results in a TTree for analysis.
Double_t eRes(Double_t eraw, Bool_t addRes = kTRUE) // Input in GeV
{
if (!addRes) {
return eraw; // Return original energy if no resolution to be added
}
// Constants for energy resolution calculation
const Double_t keVtoGeV = 1.e-6;
const Double_t GeVtokeV = 1.e6;
const Double_t sig_noise = 50.0; // keV, electronic noise term
const Double_t fano_factor = 0.12; // Fano factor
const Double_t omega = 3.6e-3; // keV/electron-hole pair
// Convert input energy to keV
const Double_t energy_keV = eraw * GeVtokeV;
// Calculate intrinsic resolution component (Fano-limited)
const Double_t sig_int = TMath::Sqrt(omega * fano_factor * energy_keV);
// Combine resolutions using direct calculation (avoiding Hypot)
const Double_t total_res = TMath::Sqrt(sig_noise*sig_noise + sig_int*sig_int);
// Generate smeared energy with protection against non-positive values
Double_t smeared_energy_keV;
do {
smeared_energy_keV = gRandom->Gaus(energy_keV, total_res);
} while (smeared_energy_keV <= 0.0);
// Convert back to GeV and return
return smeared_energy_keV * keVtoGeV;
}
TVector3 angleRes(TVector3 pvraw, bool addRes = true) // rad
{
const Double_t kDegree = TMath::Pi()/180.;
const Double_t kSigma = 1.0 * kDegree; // 1 degree resolution
if (!addRes) {
return pvraw.Unit();
}
// Get original angles
Double_t theta = pvraw.Theta();
Double_t phi = pvraw.Phi();
// Apply uniform random smearing within ±0.5σ
theta += kSigma * (gRandom->Uniform() - 0.5);
phi += kSigma * (gRandom->Uniform() - 0.5);
// Create new vector with modified angles
TVector3 modifiedVec;
modifiedVec.SetMagThetaPhi(pvraw.Mag(), theta, phi);
return modifiedVec.Unit();
}
Int_t SelectIndex(Int_t n, const Double_t* ratios) {
Double_t sum = 0;
for (Int_t i = 0; i < n; ++i) {
sum += ratios[i];
}
Double_t r = gRandom->Uniform(0, sum);
Double_t cumulative = 0;
for (Int_t i = 0; i < n; ++i) {
cumulative += ratios[i];
if (r < cumulative) {
return i;
}
}
return n - 1; // Fallback for numerical precision
}
double getMass(int zz, int aa, const char* inputFile = "mass.txt")
{
const double keV2GeV = 1.0e-6;
double mass = -1.0; // Default return value if not found
std::ifstream inFile(inputFile);
if (!inFile) {
std::cerr << "Error: Cannot open input file: " << inputFile << std::endl;
return mass;
}
int Z, A;
double m;
bool found = false;
while (inFile >> Z >> A >> m) {
if (Z == zz && A == aa) {
mass = m * keV2GeV;
found = true;
break;
}
}
if (!found) {
std::cerr << "Warning: Mass not found for Z=" << zz
<< ", A=" << aa << " in " << inputFile << std::endl;
}
return mass;
}
double a=getMass(6,12);
cout<<setprecision(12)<<a<<endl;
11.1748627384

void Simulation() {
// Ground-state masses (in GeV)
Double_t mH1 = getMass(1, 1);
Double_t mHe4 = getMass(2, 4);
Double_t mBe10 = getMass(4, 10);
Double_t mC14 = getMass(6, 14);
// Excitation energies and branching ratios
const Double_t ExBe10[2] = {0.0, 3.368}; // ^10Be ex.
const Double_t ExC14_Be10_0[3] = {14.9, 15.6, 16.4}; // ^14C ex. decaying to ^10Be gs.
const Double_t Gamma_C14_Be10_0[3] = {0.1, 0.18, 0.14}; // Widths for ^14C states decaying to ^10Be gs.
const Double_t Ratio_C14_Be10_0[3] = {0.25, 0.50, 0.25}; // BR for ^14C states to ^10Be gs. (25%, 50%, 25%)
const Double_t ExC14_Be10_1[2] = {17.3, 18.5}; // ^14C ex. decaying to ^10Be ex.
const Double_t Gamma_C14_Be10_1[2] = {0.12, 0.08}; // Widths for ^14C states decaying to ^10Be ex.
const Double_t Ratio_C14_Be10_1[2] = {0.5, 0.5}; // BR for ^14C states to ^10Be excited state (50%, 50%)
const Double_t Be10Ratio[2] = {0.5, 0.5}; // BR for ^10Be states (50% ground, 50% excited)
// Unit conversions
const Double_t GeV = 1.e-3; // MeV to GeV
const Double_t MeV = 1.e3; // GeV to MeV
// Beam parameters (energy in MeV, converted to GeV)
const Double_t ekBeamMean = 317.1; // MeV
const Double_t ekBeamSigma = 1.83 / 2.35; // MeV (FWHM to sigma)
// Beam and target
Double_t mBeam = mC14;
Double_t mTarget = mH1;
Double_t ekBeam, eBeam, pBeam;
TLorentzVector beam, target(0., 0., 0., mTarget), compound;
// Phase-space generators
TGenPhaseSpace CompoundDecay; // 1st decay: Compound -> H1 + C14*
TGenPhaseSpace C14xDecay; // 2nd decay: C14* -> He4 + Be10*
// Output variables
Double_t weight[2];
Double_t ek[3], theta[3], phi[3];
Double_t exBe10, exC14;
// Output file and tree
TFile *fout = new TFile("C14H1_He4Be10x.root", "recreate");
TTree *tree = new TTree("tree", "tree");
tree->Branch("ekBeam", &ekBeam, "ekBeam/D");
tree->Branch("ek", ek, "ek[3]/D");
tree->Branch("theta", theta, "theta[3]/D");
tree->Branch("phi", phi, "phi[3]/D");
tree->Branch("exBe10", &exBe10, "exBe10/D");
tree->Branch("exC14", &exC14, "exC14/D");
tree->Branch("weight", weight, "weight[2]/D");
// Simulation loop
for (Int_t n = 0; n < 1000000; ++n) {
// Beam energy (Gaussian distribution in GeV)
ekBeam = gRandom->Gaus(ekBeamMean * GeV, ekBeamSigma * GeV);
eBeam = ekBeam + mBeam;
pBeam = sqrt(eBeam * eBeam - mBeam * mBeam);
beam.SetPxPyPzE(0., 0., pBeam, eBeam);
// Compound system
compound = beam + target;
// 1st decay: Sample Be10 and C14 excitation energies
Int_t iBe10 = SelectIndex(2, Be10Ratio);
exBe10 = ExBe10[iBe10];
Int_t iC14;
const Int_t maxRetries = 100;
Int_t retries = 0;
if (iBe10 == 0) {
// Select C14 state (0, 1, 2) with 25%, 50%, 25% probability
iC14 = SelectIndex(3, Ratio_C14_Be10_0);
do {
exC14 = gRandom->BreitWigner(ExC14_Be10_0[iC14], Gamma_C14_Be10_0[iC14]);
++retries;
} while (exC14 >= 30.0 && retries < maxRetries);
} else {
// Select C14 state (0, 1) with 50%, 50% probability
iC14 = SelectIndex(2, Ratio_C14_Be10_1);
do {
exC14 = gRandom->BreitWigner(ExC14_Be10_1[iC14], Gamma_C14_Be10_1[iC14]);
++retries;
} while (exC14 >= 30.0 && retries < maxRetries);
}
// Skip invalid excitation energies
if (exC14 >= 30.0 || exC14 < 0.0 || exBe10 < 0.0) {
continue;
}
// Define masses for decays (in GeV)
Double_t masses_1st[2] = {mH1, mC14 + exC14 * GeV};
Double_t masses_2nd[2] = {mHe4, mBe10 + exBe10 * GeV};
// 1st decay: Compound -> H1 + C14*
if (!CompoundDecay.SetDecay(compound, 2, masses_1st)) {
std::cout << "1st decay kinematically forbidden!" << std::endl;
continue;
}
weight[0] = CompoundDecay.Generate();
if (TMath::IsNaN(weight[0]) || TMath::IsNaN(CompoundDecay.GetWtMax())) {
continue;
}
TLorentzVector *H1 = CompoundDecay.GetDecay(0);
TLorentzVector *C14x = CompoundDecay.GetDecay(1);
// 2nd decay: C14* -> He4 + Be10*
if (!C14xDecay.SetDecay(*C14x, 2, masses_2nd)) {
std::cout << "2nd decay kinematically forbidden!" << std::endl;
continue;
}
weight[1] = C14xDecay.Generate();
if (TMath::IsNaN(weight[1]) || TMath::IsNaN(C14xDecay.GetWtMax())) {
continue;
}
TLorentzVector *He4 = C14xDecay.GetDecay(0);
TLorentzVector *Be10x = C14xDecay.GetDecay(1);
// Calculate observables
TVector3 pv[3];
ek[0] = H1->E() - mH1; // Kinetic energy (GeV)
pv[0] = H1->Vect().Unit();
ek[1] = He4->E() - mHe4;
pv[1] = He4->Vect().Unit();
ek[2] = Be10x->E() - mBe10;
pv[2] = Be10x->Vect().Unit();
// Skip events with very low energy particles
bool validEnergy = true;
for (Int_t i = 0; i < 3; ++i) {
if (ek[i] < 100.e-6) { // 100 keV threshold
validEnergy = false;
break;
}
}
if (!validEnergy) {
continue;
}
// Apply experimental resolutions and convert units
for (Int_t i = 0; i < 3; ++i) {
ek[i] = eRes(ek[i]) * MeV; // Convert to MeV
pv[i] = angleRes(pv[i]);
theta[i] = pv[i].Theta();
phi[i] = pv[i].Phi();
}
ekBeam *= MeV; // Convert to MeV
tree->Fill();
if (n % 50000 == 0) {
std::cout << ".";
}
}
std::cout << std::endl;
tree->Write();
fout->Close();
}
TFile *f = new TFile("C14H1_He4Be10x.root");
TTree *tree = (TTree*)f->Get("tree");
TCanvas *c1 = new TCanvas;
c1->Clear();
c1->SetWindowSize(900,300);
c1->Divide(3,1);
c1->cd(1);
tree->Draw("ek[0]:theta[0]>>h1(200,0,0.8,300,0,60)","","colz");
gPad->SetLogz();
c1->cd(2);
tree->Draw("ek[1]:theta[1]>>h2(200,0,0.8,300,30,160)","","colz");
gPad->SetLogz();
c1->cd(3);
tree->Draw("ek[2]:theta[2]>>h3(200,0,0.8,300,50,360)","","colz");
gPad->SetLogz();
c1->Draw();
c1->Clear();
c1->SetWindowSize(900,300);
c1->Divide(3,1);
c1->cd(1);
tree->Draw("exC14>>h1(200,12,21)","exBe10<1","colz");
gPad->SetLogy();
c1->cd(2);
tree->Draw("exC14>>h2(200,12,21)","exBe10>1","colz");
gPad->SetLogy();
c1->cd(3);
tree->Draw("exBe10>>h3(200,-1,5)","","colz");
gPad->SetLogy();
c1->Draw();