4.2 二维对称矩阵的本底-Radware approch¶
二维矩阵¶
In [1]:
TCanvas *c1=new TCanvas;
TFile *fgamma=new TFile("eu152gg.root");
TH2D *hgg=(TH2D*)fgamma->Get("hgg");
hgg->Draw("colz");
gPad->SetLogz();
c1->Draw();
In [2]:
.L peaks.C
总投影谱- total projection spectrum¶
In [3]:
TH1D *hg=hgg->ProjectionX("hg");
peaks("hg");
c1->Draw();
152Eu decay¶
- X-ray - through EC of 152Eu follows by the emission of a characterisitic x-ray of 152Sm
| X-ray | Energy(keV) | Intensity |
|---|---|---|
| XR kα2 | 39.522 | 21.0 % |
| XR kα1 | 40.118 | 37.7 % |
| XR kβ3 | 45.293 | 3.75 % |
| XR kβ1 | 45.414 | 7.26 % |
| XR kβ2 | 46.578 | 2.40 % |
- $\gamma -$ ray 参考 作业4.1内衰变纲图
总投影谱的peaks和background¶
In [4]:
TSpectrum *sa=new TSpectrum(200);
TH1D *hbg,*hpeak;
//Generate Smooth Background under peaks.
hbg=(TH1D*)sa->Background(hg,8,"nosmoothing same");//background
hbg->SetFillColor(kWhite);
hpeak=new TH1D("hpeak","hpeak",1500,0,1500);
hpeak->Add(hg,hbg,1,-1);//peaks
hpeak->SetLineColor(kBlack);
hpeak->Draw("same");
gPad->SetLogy();
c1->Draw();
Radware method：Background Substraction in $M_{ij}$ gg matrix¶
- D.C. Radford, Nucl. Instr. Meth. A361(1995)306
For $i_{th}$ bin of the total 1D projection of two-fold coincidence matrix $M_{ij}$, the total counts $𝑃_i$ can be divided into a “background” spectrum $b_i$ and a “peak” spectrum $p_i$ : $P_i=b_i+p_i$。The background counts underlying the peaks arise from both Compton-scattered γ-rays and quasi-continuum transitions.
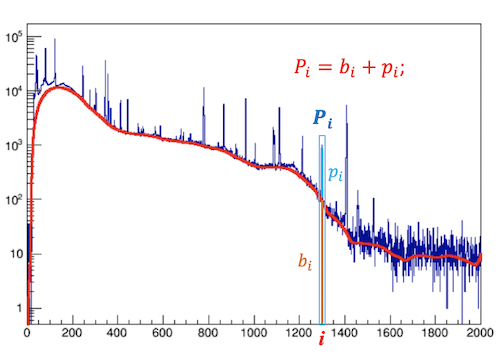$$P_i=\sum_{j} M_{ij}, \quad T=\sum_{j}P_j $$
For the two-fold background matrix $B_{ij}$:
$$b_i=\sum_{j} B_{ij} $$$$b_i= b_i \frac{\sum_{j} P_j}{T} =\sum_{j}{\frac{1}{T} b_i P_j}$$$$B_{ij}=\frac{1}{T}b_i P_j=\frac{1}{T}b_i(p_j+b_j)=\frac{1}{T}(b_i p_j+b_i b_j)$$
But the term of $b_j p_i$ is not include in the equation above, so that $B_{ij}$ is asymmetric. The symmetric 2D background can be written as: $$B_{ij}=\frac{1}{T}(b_i p_j+b_j p_i+b_i b_j)=\frac{1}{T}(P_i P_j-p_i p_j)$$
- 上述方法可以推广到 3-fold，4-fold的矩阵
其他方法：¶
- G. Palameta and J.C. Waddington, Nucl. Instr. Meth. A234(1985)476
- TSpectrum2的Background()方法
Radware方法的具体实现¶
In [5]:
TH2D* hggb=new TH2D("hggb","bgmat for gg",1500,0,1500,1500,0,1500);
TH2D* hggmat=new TH2D("hggmat","ggmat with backsub",1500,0,1500,1500,0,1500);
Double_t T,Pi,Pj,pi,pj,Bij,x,y;
In [6]:
T=hg->Integral();
for(int i=0;i<hgg->GetNbinsX();i++) {
for(int j=0;j<hgg->GetNbinsY();j++) {
Pi=hg->GetBinContent(i+1);
Pj=hg->GetBinContent(j+1);
pi=hpeak->GetBinContent(i+1);
pj=hpeak->GetBinContent(j+1);
Bij=(Pi*Pj-pi*pj)/T;
if(Bij<0) Bij=0;
x=hg->GetBinCenter(i+1);
y=hg->GetBinCenter(j+1);
hggb->Fill(x,y,Bij);// backgound gg matix
}
}
hggmat->Add(hgg,hggb,1,-1);// background subtracted gg matix.
本底$\gamma-\gamma$矩阵¶
In [7]:
hggb->Draw("colz");
c1->SetLogy(0);
c1->SetLogz();
c1->Draw();
减本底后的$\gamma-\gamma$矩阵¶
In [8]:
hggmat->Draw("colz");
c1->SetLogy(0);
c1->SetLogz();
c1->Draw();
In [9]:
TH1D *hgx=hggmat->ProjectionX("hgx");
peaks("hgx");
c1->Draw();
观察矩阵的局部¶
In [10]:
.L zoom.C
In [11]:
zoom("hgg",70,70,100);
c1->Draw();//Draw(“surf1”);
In [12]:
zoom("hggb",70,70,100);
c1->Draw();
In [13]:
zoom("hggmat",70,70,100);
c1->Draw();
c1->Draw();
In [14]:
void gate(Double_t ge, TH2D* hgg, Double_t xmax=1500,Double_t gew=2)
{ int ih=0;
double gea,geb;
TH1D *hg;
TString hname;
hgg->SetAxisRange(0,xmax,"X");
hgg->SetAxisRange(0,xmax,"Y");
gea=hgg->GetXaxis()->FindBin(ge-gew);
geb=hgg->GetXaxis()->FindBin(ge+gew);
hname.Form("gated on %d keV_%i",int(ge),ih++);
hg=hgg->ProjectionX(hname,gea,geb);
hg->SetTitle(hname);
hg->Sumw2(0);
hg->SetAxisRange(0,1500,"X");
peaks(hname,0.02);
c1->Draw();
}
122keV的开窗谱¶
- 152Eu中和121keV有符合的gamma射线：244、296、444 ... keV
In [15]:
gate(122.5,hggmat);
Interactive Generation of level scheme¶
- Assume a tentative level scheme with branching ratios for different transitions
- Predict the projected spectra in coincidence with gates
- Compare with the observed intensity of g-lines
- Adjust branching ratios to fit counts in peak
- Add new levels & transitions if required
- Continue until satisfied !!
- Spin & parity from angular correlation/polarization data
验证133Ba的衰变纲图¶
x-ray¶
- through EC of 133Ba follows by the emission of a characterisitic x-ray of 133Cs
| X-ray | Energy(keV) | Intensity |
|---|---|---|
| XR kα2 | 30.625 | 33.9 % |
| XR kα1 | 30.973 | 62.2 % |
| XR kβ3 | 34.92 | 5.88 % |
| XR kβ1 | 34.987 | 11.4 % |
| XR kβ2 | 35.818 | 3.51 % |
$\gamma-$ ray¶
Each level decay through $\gamma$ and IC(Internal Conversion) with intensity of $I_{\gamma}$ and $I_{e}$, respectively.
预期符合关系¶
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | x | x | O | x | x | O | O | x |
| 302 | O | x | x | x | x | O | x | x |
| 383 | O | x | x | x | x | O | x | x |
| 53 | O | O | O | O | O | x | x | x |
| 276 | O | O | x | x | x | x | x | x |
| 356 | O | x | x | x | x | x | x | x |
In [16]:
//%jsroot on
gate(80,hggmat,400);//80:53,80!,223,276,302,356, no 160!
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
In [17]:
gate(223,hggmat,400);//223:53,80,160 -> 80+80=160
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
In [18]:
gate(160,hggmat,400);//160:53,80,276
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | O->x | x | O | x | x | O | O | x |
gate(80)没有160峰，gate(160)有80峰：80和160没有符合
In [19]:
gate(302,hggmat,400);//302:53,80
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | O->x | x | O | x | x | O | O | x |
| 302 | O | x | x | x | x | O | x | x |
In [20]:
gate(383,hggmat,400);//383:53
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | O->x | x | O | x | x | O | O | x |
| 302 | O | x | x | x | x | O | x | x |
| 383 | O | x | x | x | x | O | x | x |
In [21]:
gate(53,hggmat,400);//53:80,223,302,383: 223+80=302, 80+302=382,
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | O->x | x | O | x | x | O->x | O | x |
| 302 | O | x | x | x | x | O | x | x |
| 383 | O | x | x | x | x | O | x | x |
| 53 | O | x | O | O | O | x | O | x |
In [22]:
gate(276,hggmat,400);//276:80,160
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | O->x | x | O | x | x | O->x | O | x |
| 302 | O | x | x | x | x | O | x | x |
| 383 | O | x | x | x | x | O | x | x |
| 53 | O | x->O | O | O | O | x | O->x | x |
| 276 | O | O | x | x | x | x | x | x |
- 276-53没有符合！
In [23]:
gate(356,hggmat,400);//356:80
观察符合得到的关联关系¶
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | O->x | x | O | x | x | O->x | O | x |
| 302 | O | x | x | x | x | O | x | x |
| 383 | O | x | x | x | x | O | x | x |
| 53 | O | x->O | O | O | O | x | O->x | x |
| 276 | O | O | x | x | x | x | x | x |
| 356 | O | x | x | x | x | x | x | x |
预期符合关系¶
| gate \ peaks | 80 | 160 | 223 | 302 | 383 | 53 | 276 | 356 |
|---|---|---|---|---|---|---|---|---|
| 80 | O | x | O | O | x | O | O | O |
| 223 | O | O | x | x | x | O | x | x |
| 160 | x | x | O | x | x | O | O | x |
| 302 | O | x | x | x | x | O | x | x |
| 383 | O | x | x | x | x | O | x | x |
| 53 | O | O | O | O | O | x | x | x |
| 276 | O | O | x | x | x | x | x | x |
| 356 | O | x | x | x | x | x | x | x |
说明¶
53keV与160keV的符合关系与预期不一致。
当两个gamma之间相隔越远(中间相隔的gamma较多)时，由于中间路径中其他gamma分流强度，两者之间的符合强度很小。 当统计不强的时候，不容易看见他们之间的直接符合。 因此gamma开窗谱，一般用于确定相隔不远的gamma之间的符合关系。 根据附近gamma之间的关联，以及gamma能量之间的加合和强度平衡关系，猜测可能的符合关系。按照上述步骤，逐步验证和修订，最终建立能级纲图。
一般同轴型HPGe的效率在200keV附近为峰值，在50keV附近效率很低。
- 根据上述讨论和实际观察到的gamma之间的关联，可以确认53keV-160keV有符合关系。
- 二维，三维γ矩阵分析程序 GATE2，GATE3：https://github.com/zhihuanli/gamma-gamma-coincidence-analysis
偶然符合矩阵¶
在熔合蒸发反应γ谱学实验中，低能区通常会观察到来自实验靶的衬底成分（如Au或Pb）的X射线峰，例如图b、c中的68、79和279keV附近的峰。这些X射线是由于被束流激发的衬底原子在退激时产生的。与熔合蒸发反应产物的γ-γ之间不同的是，X射线和γ射线之间没有符合关系（不相关）。然而，由于X射线的生成截面远大于γ射线的生成截面，在γ−γ符合时间窗内会混入显著的偶然符合成分(见图a)。
可以通过构建偶然符合矩阵，按照下述步骤去除符合时间窗内的偶然符合成分。
首先，将符合时间窗范围内的γ符合事件填入瞬发符合矩阵PAM（Prompt+Accindental Matrix）中。然后，在符合时间窗范围外选取左右对称的两个偶然符合时间窗（图a中红色阴影区），将该区域的事件填入偶然符合本底矩阵AM（Accindental Matrix）。通过将PAM矩阵减去AM矩阵得到最终的矩阵PM（Prompt Matrix）：设符合时间窗长度为dPT，偶然符合窗总长度dAT，则 PM = PAM - (dPT/dAT) * AM。
经验表明，所选偶然符合时间窗距离符合时间窗越近，其偶然符合事件的扣除效果越好。原则上，偶然符合时间窗的选择应紧挨着符合时间窗的两个对称时间窗。图b和c展示了扣除偶然符合前后的投影谱对比图。粉色表示未扣除偶然符合的投影谱，而蓝色表示扣除偶然符合后的投影谱。可以看出，通过偶然符合的扣除，197Au的X射线影响大大减少。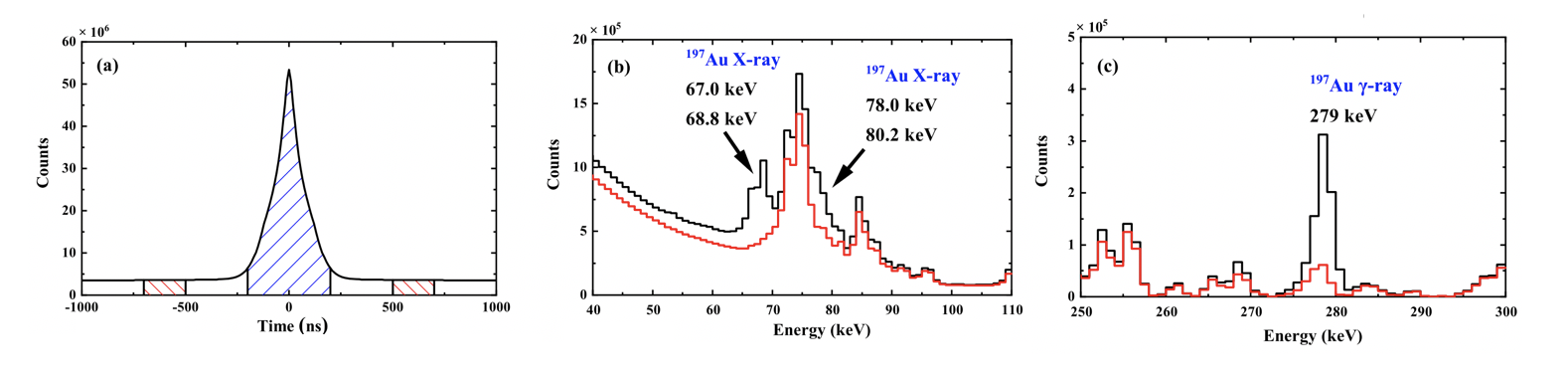
- AM矩阵可以按照上述Radware方法进行进一步分析。
- 参考文献：D.W. Luo, H.Y. Wu et al., NUCL. SCI. TECH. 32,79 (2021) https://link.springer.com/article/10.1007/s41365-021-00917-8 ## 演示如何在NNDC网站中查询某一核素的$\gamma$射线能量信息，$\gamma-\gamma$符合信息。
- www.nndc.bnl.gov