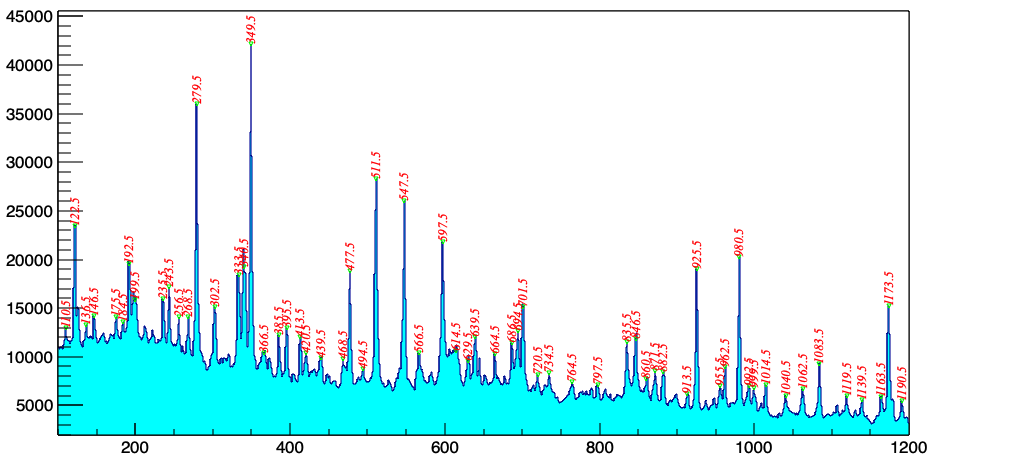
4.1 $\gamma - \gamma$ 二维对称矩阵-I¶

  1. gamma-gamma符合分析方法
  2. 二维对称矩阵减本底方法

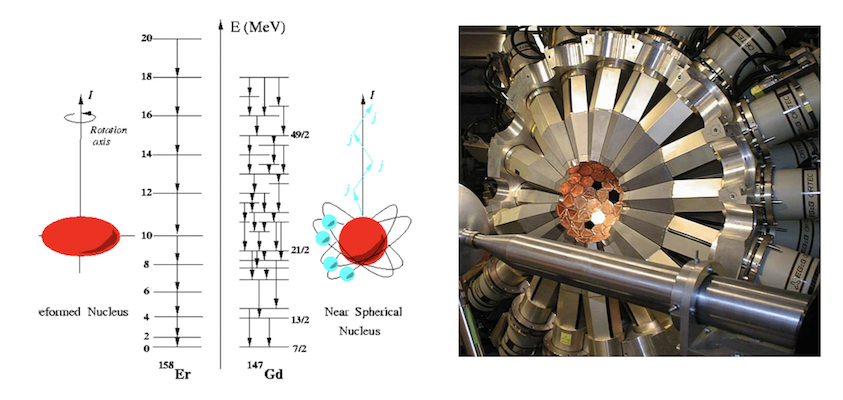
  • Data
    • eurica.root
    • Branch：ahit, aid[ahit], ae[ahit], at[ahit]
In [1]:
TCanvas *c1=new TCanvas("c1","c1");
TFile *fin=new TFile("eurica.root");
TTree *tree=(TTree*) fin->Get("tree");

能谱¶

In [2]:
.L peaks.C
In [3]:
tree->Draw("ae>>hae(1500,0,1500)");
peaks("hae");
c1->SetLogy();
c1->Draw();

addback hit¶

  • aid 取为以同一探测探测器有符合的相邻探测单元中时间最快的单元的id
In [4]:
tree->Scan("aid:int(ae):int(at/25):gid:int(gid/7):int(ge):int(gt/25)","","",5,0);

***********************************************************************************************************
*    Row   * Instance *       aid *   int(ae) * int(at/25 *       gid * int(gid/7 *   int(ge) * int(gt/25 *
***********************************************************************************************************
*        0 *        0 *         0 *        93 *     -2699 *         2 *         0 *        93 *     -2698 *
*        0 *        1 *        14 *       513 *     -1543 *        14 *         2 *       513 *     -1543 *
*        0 *        2 *        35 *       255 *      -460 *        41 *         5 *       255 *      -461 *
*        0 *        3 *        42 *       191 *      -462 *        48 *         6 *       191 *      -462 *
*        0 *        4 *        70 *       900 *      -645 *        76 *        10 *       900 *      -644 *
*        1 *        0 *        35 *       355 *      -682 *        38 *         5 *       355 *      -682 *
*        1 *        1 *        77 *       252 *     -2083 *        78 *        11 *       252 *     -2083 *
*        2 *        0 *        28 *       166 *      -708 *        22 *         3 *       721 *      -932 *
*        2 *        1 *        28 *        73 *       170 *        24 *         3 *        69 *      -933 *
*        2 *        2 *        35 *       856 *      -705 *        27 *         3 *       187 *      -931 *
*        2 *        3 *        35 *       121 *      -200 *        28 *         4 *       166 *      -709 *
*        2 *        4 *        42 *       257 *      -202 *        32 *         4 *        73 *       169 *
*        2 *        5 *        77 *      1275 *     -3369 *        37 *         5 *       856 *      -706 *
*        2 *        6 *           *           *           *        41 *         5 *       121 *      -201 *
*        2 *        7 *           *           *           *        44 *         6 *       257 *      -202 *
*        2 *        8 *           *           *           *        79 *        11 *       679 *     -3369 *
*        2 *        9 *           *           *           *        80 *        11 *       595 *     -3370 *
*        3 *        0 *         0 *       345 *     -3541 *         4 *         0 *       345 *     -3541 *
*        3 *        1 *        14 *        94 *     -3548 *        17 *         2 *        94 *     -3549 *
*        4 *        0 *         0 *       287 *     -3672 *         5 *         0 *       287 *     -3671 *
*        4 *        1 *         7 *       302 *      -766 *         8 *         1 *       302 *      -766 *
*        4 *        2 *        63 *        37 *     -1477 *        69 *         9 *        37 *     -1477 *
***********************************************************************************************************

检验探测器之间的能量关联¶

In [5]:
tree->SetAlias("at","at-(-32+2.387e3/pow(ae,0.5)-4.2658e4/pow(ae,1)+9.8122e5/pow(ae,2))");
tree->SetAlias("at0","at[0]-(-32+2.387e3/pow(ae[0],0.5)-4.2658e4/pow(ae[0],1)+9.8122e5/pow(ae[0],2))");
tree->SetAlias("at1","at[1]-(-32+2.387e3/pow(ae[1],0.5)-4.2658e4/pow(ae[1],1)+9.8122e5/pow(ae[1],2))");
In [6]:
TCut atcoin="abs(at0-at1)<180";
TCut adet="aid[0] != aid[1]";
tree->Draw("ae[0]:ae[1]>>(1000,0,1000,1000,0,1000)",adet&&atcoin,"colz");
c1->SetLogy(0);
c1->SetLogz();
c1->Draw();

与121keV符合的gamma能谱¶

  • 需要分别检查多重性的所有组合。
    • ae[0] with conditions: "abs(ae[1]-121)<2 || "abs(ae[2]-121)<2 ..."
    • ae[1] with conditions: "abs(ae[0]-121)<2 || "abs(ae[2]-121)<2 ..."
    • ...
In [7]:
tree->Draw("ae[0]>>he0(1000,0,1000)","abs(ae[1]-121)<2 || abs(ae[2]-121)<2" && adet&&atcoin,"goff");
tree->Draw("ae[1]>>he1(1000,0,1000)","abs(ae[0]-121)<2 || abs(ae[2]-121)<2" && adet&&atcoin,"goff");
TH1D *he0 = (TH1D*)gROOT->FindObject("he0");
TH1D *he1 = (TH1D*)gROOT->FindObject("he1");
he0->SetLineColor(kRed);
he1->Draw();
he0->Draw("same");
c1->SetLogy(0);
c1->Draw();

二维$\gamma-\gamma$对称矩阵方法¶

  • In a multi-detector array, detectors placed at different angles are essentially equivalent ( ignoring $\theta, \phi$ dependence)
  • In the analysis of data from such arrays, one often creates two-dimensional histograms from double-coincidence data, or three-dimensional histograms from triple-coincidence data, and then proceeds to set ''gates'', i.e. specify energies for all but one of the axes and inspect the projection onto the remaining axis.

上述方法有时称之为拆对符合¶

gamma-gamma 二维关联¶

保留tree结构¶

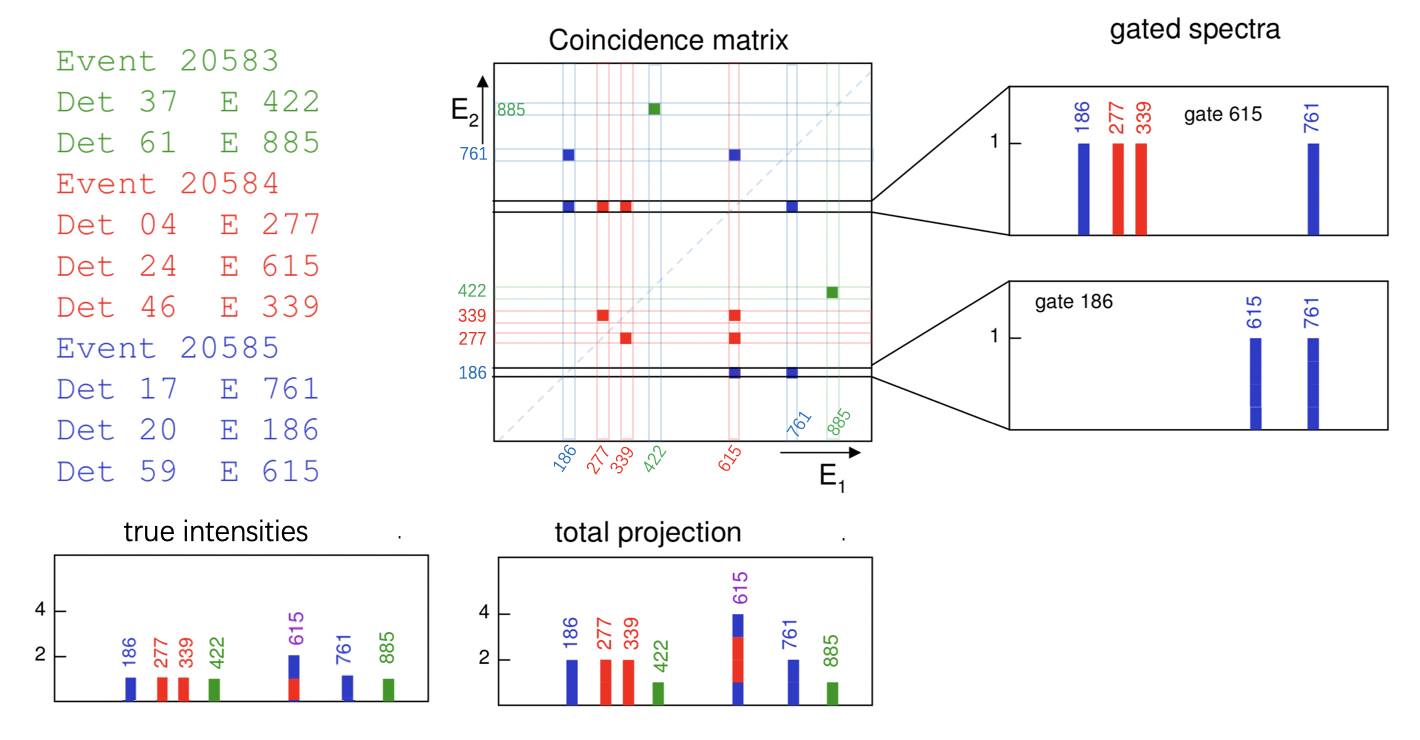
void ggmatrix()
{  
  //input
  TFile* f=new TFile("addback.root");
  TTree* tree=(TTree*)f->Get("tree");

  Int_t ahit;
  Int_t adet[1000];
  Double_t ae[1000];
  Long64_t at[1000];

  tree->SetBranchAddress("ahit", &ahit);
  tree->SetBranchAddress("ae", &ae);
  tree->SetBranchAddress("at", &at); // at 已进行timwalk修正
  tree->SetBranchAddress("adet", &adet);

  TFile *fout = new TFile("ggmatrix.root","recreate");
  TTree* tout = new TTree("tree","event");

  Int_t achit;
  Double_t aex[1000],aey[1000];
  Long64_t atx[1000],aty[1000];
  Int_t aidx[1000],aidy[1000];

  tout->Branch("achit", &achit, "achit/I");
  tout->Branch("aex", &aex, "aex[achit]/D");
  tout->Branch("aey", &aey, "aey[achit]/D");  
  tout->Branch("atx", &atx, "atx[achit]/L");
  tout->Branch("aty", &aty, "aty[achit]/L");
  tout->Branch("aidx", &aidx, "aidx[achit]/I");
  tout->Branch("aidy", &aidy, "aidy[achit]/I");

  Long64_t nentries = tree->GetEntriesFast();
  for (Long64_t jentry=0; jentry<nentries; jentry++) {
    tree->GetEntry(jentry);
    achit=0;
    for(int i=0; i<ahit; i++) {
      for(int j=0; j<ahit; j++) {
    if(i==j) continue;
    //适当放宽时间差范围，以便观察不同时间差的影响。
    if(abs(at[i]-at[j])>1000) continue; 
    aidx[achit]=adet[i];
    aidy[achit]=adet[j];
    aex[achit]=ae[i];
    aey[achit]=ae[j];
    atx[achit]=at[i];
    aty[achit]=at[j];
    achit++;
      }
    }
    if(achit>0) tout->Fill();

    if((jentry) % Long64_t(1e3) == 0) {
      printf("Process %.2f %%, %5d k / %5d k \r",Double_t(jentry)/nentries*100.,
         int(jentry/1000), int(nentries/1000));
      fflush(stdout);
    }
  }
  cout<<endl;
  tout->Write();
  fout->Close();
}

直接生成二维矩阵¶

TH2D *hgg=new TH2D("hgg","g-g matrix",1500,0,1500,1500,0,1500);
 ... ...
     for(int i=0; i<ahit; i++) {
        for(int j=0; j<ahit; j++) {
            if(i==j) continue;
            if(abs(at[i]-at[j]>200) continue;
            hgg->Fill(ae[i],ae[j]);
        }
     }

二维$\gamma - \gamma$ 矩阵¶

  • 按照上述方法从Eurica.root文件生成ebc01.root文件
In [8]:
TFile *fg=new TFile("ebc01.root");
TTree *tree=(TTree*) fg->Get("tree");
//gStyle->SetPalette(1);
In [9]:
tree->Scan("aex:aey:atx:aty:aidx:aidy:achit","","",5,0);

***********************************************************************************************************
*    Row   * Instance *       aex *       aey *       atx *       aty *      aidx *      aidy *     achit *
***********************************************************************************************************
*        0 *        0 * 255.53135 * 191.77148 * -11531.70 * -11581.70 *        35 *        42 *         2 *
*        0 *        1 * 191.77148 * 255.53135 * -11581.70 * -11531.70 *        42 *        35 *         2 *
*        1 *        0 * 166.66362 * 856.34057 * -17743.50 * -17668.50 *        28 *        35 *         4 *
*        1 *        1 * 856.34057 * 166.66362 * -17668.50 * -17743.50 *        35 *        28 *         4 *
*        1 *        2 * 121.93160 * 257.20986 * -5043.501 * -5068.501 *        35 *        42 *         4 *
*        1 *        3 * 257.20986 * 121.93160 * -5068.501 * -5043.501 *        42 *        35 *         4 *
*        2 *        0 * 345.00680 * 94.129310 * -88554.60 * -88729.60 *         0 *        14 *         2 *
*        2 *        1 * 94.129310 * 345.00680 * -88729.60 * -88554.60 *        14 *         0 *         2 *
*        3 *        0 * 877.88879 * 120.95774 * -86323.00 * -86398.00 *         0 *         7 *         8 *
*        3 *        1 * 877.88879 * 122.74848 * -86323.00 * -86498.00 *         0 *        77 *         8 *
*        3 *        2 * 120.95774 * 877.88879 * -86398.00 * -86323.00 *         7 *         0 *         8 *
*        3 *        3 * 120.95774 * 122.74848 * -86398.00 * -86498.00 *         7 *        77 *         8 *
*        3 *        4 * 976.02716 * 423.50680 * -27810.50 * -27898.00 *        42 *        56 *         8 *
*        3 *        5 * 423.50680 * 976.02716 * -27898.00 * -27810.50 *        56 *        42 *         8 *
*        3 *        6 * 122.74848 * 877.88879 * -86498.00 * -86323.00 *        77 *         0 *         8 *
*        3 *        7 * 122.74848 * 120.95774 * -86498.00 * -86398.00 *        77 *         7 *         8 *
*        4 *        0 * 193.22221 * 225.68496 * -57965.04 * -58715.04 *        14 *        70 *         2 *
*        4 *        1 * 225.68496 * 193.22221 * -58715.04 * -57965.04 *        70 *        14 *         2 *
***********************************************************************************************************

gamma-gamma 关联¶

符合时间窗外-偶然符合¶

In [10]:
tree->SetAlias("atx","at[0]-(-32+2.387e3/pow(aex,0.5)-4.2658e4/pow(aex,1)+9.8122e5/pow(aex,2))");
tree->SetAlias("aty","at[1]-(-32+2.387e3/pow(aey,0.5)-4.2658e4/pow(aey,1)+9.8122e5/pow(aey,2))");
In [11]:
TCut axycoin="abs(atx-aty)<180";
tree->Draw("aex:aey>>(1000,0,1000,1000,0,1000)",!axycoin,"colz");
c1->SetLogy(0);
c1->SetLogz();
c1->Draw();

符合时间窗内¶

In [12]:
tree->Draw("aex:aey>>hgg(1000,0,1000,1000,0,1000)",axycoin,"colz");
c1->SetLogy(0);
c1->SetLogz();
c1->Draw();
  • 二维图中部分$E_x=E_y$的交叉点仍存在，还有很多交叉点目测为偶然符合引起。
    • 以(121,121)为例，该交叉点是由(121,244),(121,444)中能量大于244，444的gamma的康普顿平台引起的。
  • (121,343)是由(780，343)符合关系中780的康普顿平台引起的。
  • (121,780)是由(343，780)符合关系中343的康普顿平台引起的。

总投影谱¶

  • 在$\gamma$谱学中称二维对称矩阵的一维投影谱为总投影谱 (Total projection spectrum)
In [13]:
tree->Draw("aex>>hxe(1000,0,1000)",axycoin,"colz");
peaks("hxe");
c1->Draw();

观察与121keV(152Eu)符合的gamma能量¶

In [14]:
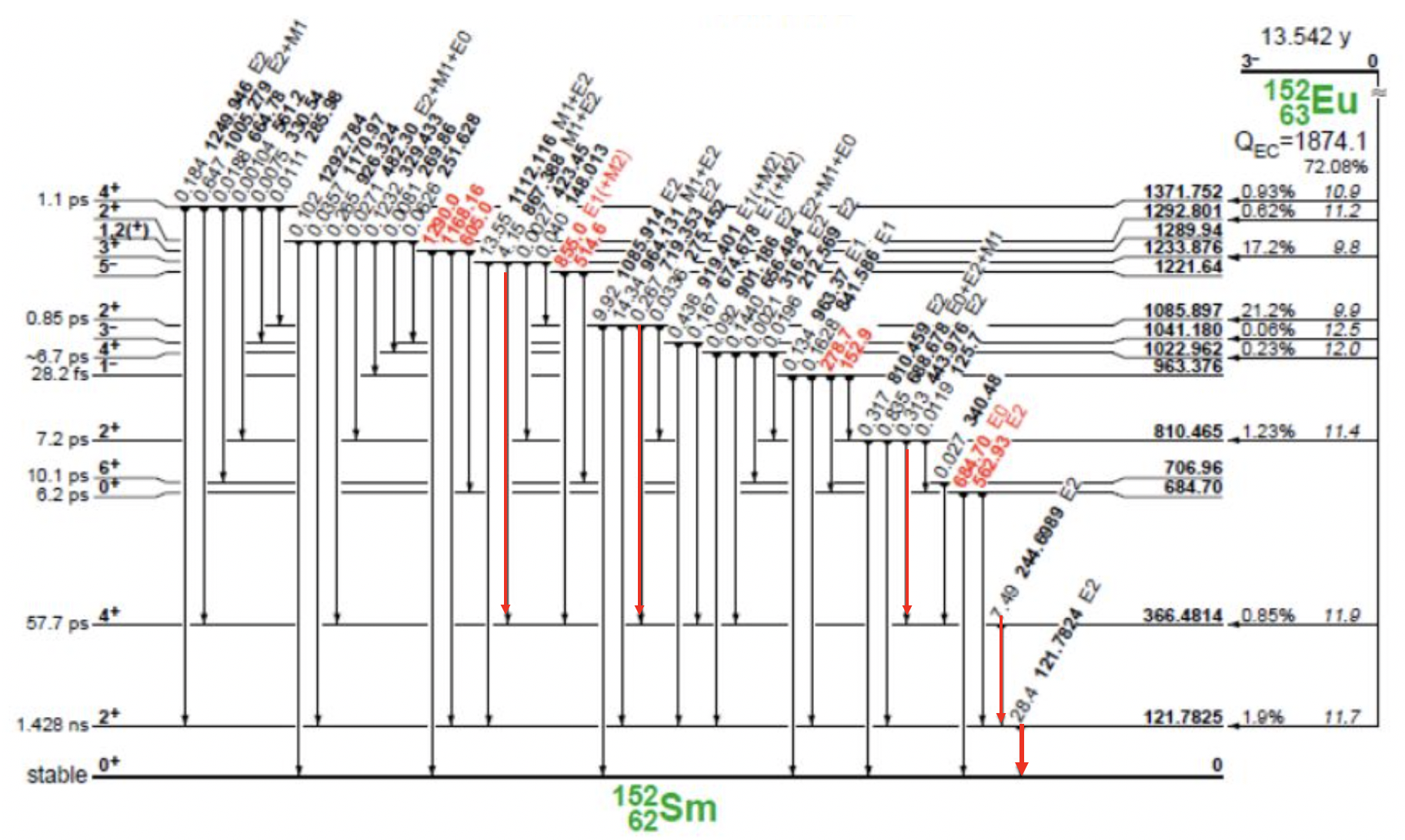
tree->Draw("aex:aey>>hgg(300,0,300,1000,0,1000)",axycoin,"colz");
   TLine *line = new TLine(117,1000,117,0);
   line->SetLineColor(kRed);
   line->Draw();
   line = new TLine(125,1000,125,0);
   line->SetLineColor(kRed);
   line->Draw();

   line = new TLine(113,1000,113,0);
   line->SetLineColor(kYellow);
   line->Draw();
   line = new TLine(105,1000,105,0);
   line->SetLineColor(kYellow);
   line->Draw();

   line = new TLine(129,1000,129,0);
   line->SetLineColor(kYellow);
   line->Draw();
   line = new TLine(137,1000,137,0);
   line->SetLineColor(kYellow);
   line->Draw();
c1->SetLogy(0);

c1->SetLogz();
c1->Draw();

152Eu中和121keV有符合的gamma射线：40,244、444 ... keV - 红色直线之间较亮的横线。 开窗谱中出现 80keV(133Ba)，121keV(!)等不与之符合的gamma峰 - 偶然符合 - 红色直线之间的横线，且与周围黄线之间的横线亮度相同。

总投影谱上的开窗区域¶

In [15]:
peaks("hxe");
Int_t a1 = hxe->GetBinContent(hxe->FindBin(117));
TLine *line = new TLine(117,a1,117,0);
line->SetLineColor(kRed);
line->Draw();
a1 = hxe->GetBinContent(hxe->FindBin(125));
line = new TLine(125,a1,125,0);
line->SetLineColor(kRed);
line->Draw();
a1 = hxe->GetBinContent(hxe->FindBin(113));
line = new TLine(113,a1,113,0);
line->SetLineColor(kYellow);
line->Draw();
a1 = hxe->GetBinContent(hxe->FindBin(105));
line = new TLine(105,a1,105,0);
line->SetLineColor(kYellow);
line->Draw();
a1 = hxe->GetBinContent(hxe->FindBin(129));
line = new TLine(129,a1,129,0);
line->SetLineColor(kYellow);
line->Draw();
a1 = hxe->GetBinContent(hxe->FindBin(137));
line = new TLine(137,a1,137,0);
line->SetLineColor(kYellow);
line->Draw();
c1->Draw();
In [16]:
TCut axe121="abs(aex-121)<2";//能量cut的范围取决于对应能量下的能量分辨。
tree->Draw("aey>>hye(1000,0,1000)",axe121&&axycoin,"colz");
TH1D *hye=(TH1D*)gROOT->FindObject("hye");
peaks("hye");
c1->Draw();

从峰两侧估计compton平台对符合谱的贡献¶

  • 从总投影谱上看121keV的左右两侧有平坦区域。
  • 基于不同的考虑，可以只选择左侧或右侧本底。
  • 如果峰的周围不存在平坦区域，可选择相邻的峰的平坦区域来作为本底的近似。
  • 注意二维谱中斜线区域(康普顿能量关联)在不同范围的开窗谱中的影响。

峰左侧连续平台开窗(gate)¶

In [17]:
TCut axe121Left="abs(aex-121-5)<2";
tree->Draw("aey>>hyel(1000,0,1000)",axe121Left&&axycoin,"colz");
TH1D *hyel=(TH1D*)gROOT->FindObject("hyel");
peaks("hyel");
c1->Draw();

峰右侧连续平台开窗¶

In [18]:
TCut axe121Right="abs(aex-121+5)<2";
tree->Draw("aey>>hyer(1000,0,1000)",axe121Right&&axycoin,"colz");
TH1D *hyer=(TH1D*)gROOT->FindObject("hyer");
peaks("hyer");
c1->Draw();

减去121keV峰下compton本底贡献¶

  • 假设本底分布是线性的，左右本底各贡献一半。
In [19]:
TH1D *hbkg = new TH1D("hbkg","background",1000,0,1000);
hbkg->Add(hyel,hyer,0.5,0.5);
hbkg->SetLineColor(kBlack);
peaks("hye");
hye->SetMinimum(50);
hbkg->Draw("same");
c1->SetLogy();
c1->Draw();

减本底后的开窗谱¶

  • 偶然符合导致的本底基本被减掉。
  • 152Eu中和121keV有符合的gamma射线：244、296、444 ... keV
In [20]:
hye->Add(hye,hbkg,1,-1);
hye->Sumw2(0);
hye->SetMinimum(500);
peaks("hye");
c1->Draw();

总结¶

  • 可以通过在平坦区域开窗，减去Compton本底的贡献，得到正确的符合关系。

    • 如果峰下本底面积Npb与估计本底面积Nb不一致，则对本底谱进行归一后相减： hye->Add(hye,hbkg,1,-(Npb/Nb));

  • 该方法是二维对称矩阵见本底的最基本的方法,推荐使用上述方法。

  • 在gamma峰的密度很高的情况下，大部分gamma峰两侧找不到平坦区域，因此上述方法不可用。

  • 如：熔合蒸发反应生成的复合核布局的高自旋态退激得到的gamma谱：

  • 需要寻找更简便的方法