3.5 DSSD front-back Correlation(II) - dssd1¶
Purpose:¶
- Based on the x-y correlation, normalize the amplitudes of all strips using the amplitude of a given strip as a reference.
Normalization¶
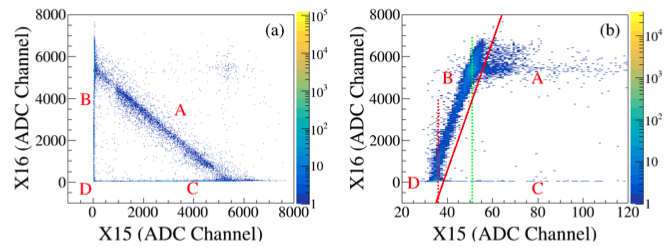
For a particle depositing energy $E$ at the intersection $(x_i, y_j)$ in a DSSD, the raw signal amplitudes $a_{xi}$ (from front strip $x_i$) and $a_{yj}$ (from back strip $y_j$) satisfy a linear relationship: $$ a_{xi} = k_{yj} a_{yj} + b_{yj}, $$ where $k_{yj}$ and $b_{yj}$ are normalization coefficients derived from energy calibration.
The goal is to normalize the amplitudes of all x- and y-strips relative to a reference strip (e.g., $x_i$) to ensure a consistent energy scale across the detector. This involves determining linear coefficients that align each strip’s amplitude to the reference.
Method 1: Pixel Normalization¶
Select a Reference Strip: Fix $x_i^*$ as the reference strip. For each y-strip $y_j$ ($j = 0, 1, \dots, N_y$), use the linear relationship:
$$ a_{xi^*} = k_{yj} a_{yj} + b_{yj}, $$to obtain normalization coefficients $\{ k_{yj}, b_{yj} \}$ by fitting events at the $(x_i, y_j)$ pixel. Sufficient event statistics are required for each pixel.
Normalize Y-Strips: Apply the coefficients to normalize all y-strip amplitudes:
$$ a_{yj}' = k_{yj} a_{yj} + b_{yj}, \quad j = 0, 1, \dots, N_y. $$Normalize X-Strips: Select a normalized y-strip (e.g., $y_j^*$) as the new reference. For each x-strip $x_k$ ($k = 0, 1, \dots, N_x$), fit:
$$ a'_{yj*} = k_{xk} a_{xk} + b_{xk}, $$to obtain coefficients $\{ k_{xk}, b_{xk} \}$ and normalize x-strip amplitudes:
$$ a'_{xk} = k_{xk} a_{xk} + b_{xk}. $$
After these steps, all x- and y-strip amplitudes are normalized to the energy scale of the initial reference strip $x_i$. This method relies on sufficient event statistics at each $(x_i, y_j)$ pixel for accurate fitting.
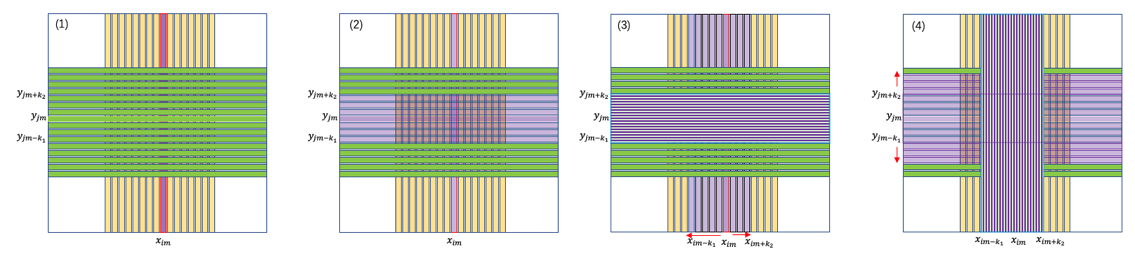
Method 2: Strip Normalization¶
This method normalizes a DSSD by starting with the strips that detect the most particles and gradually normalizing others, ensuring all strips measure energy consistently.
Identify High-Statistics Strips: Select the x-strip $x_{i^*}$ or y-strip $y_{j^*}$ with the highest event counts, typically in the detector’s central or most active regions.
Normalize Back Strips: Use $x_{i^*}$ as the reference to normalize nearby back strips $y_j$ (those close to $y_{j^*}$ with enough hits). For each $y_j$, fit the relationship:
$$ a_{x_{i^*}} = k_{yj} a_{yj} + b_{yj}, $$to find coefficients $k_{yj}$ and $b_{yj}$. Then normalize the back strip signals:
$$ a'_{yj} = k_{yj} a_{yj} + b_{yj}. $$Normalize Front Strips: Group the normalized back strips (from $y_j$ near $y_{j^*}$) into a single reference $y_{js}'$, like a wider strip. Use this to normalize nearby front strips $x_i$ (those close to $x_{i^*}$ with enough hits). For each $x_i$, fit:
$$ a'_{yj_s} = k_{xi} a_{xi} + b_{xi}, $$to find coefficients $k_{xi}$ and $b_{xi}$. Then normalize the front strip signals:
$$ a'_{xi} = k_{xi} a_{xi} + b_{xi}. $$Spread Outward: Repeat the process, using newly normalized front or back strips as references to normalize strips farther out. Continue until all strips are normalized, ensuring enough particle hits for accurate fitting at each step.
DSSD1 Normalization¶
The following analysis, using DSSD1 as an example, applies Method 2 to normalize amplitudes using coefficients $k_{yj}$ and $b_{yj}$ for y-strips and $k_{xi}$ and $b_{xi}$ for x-strips, achieving a consistent energy scale across strips.