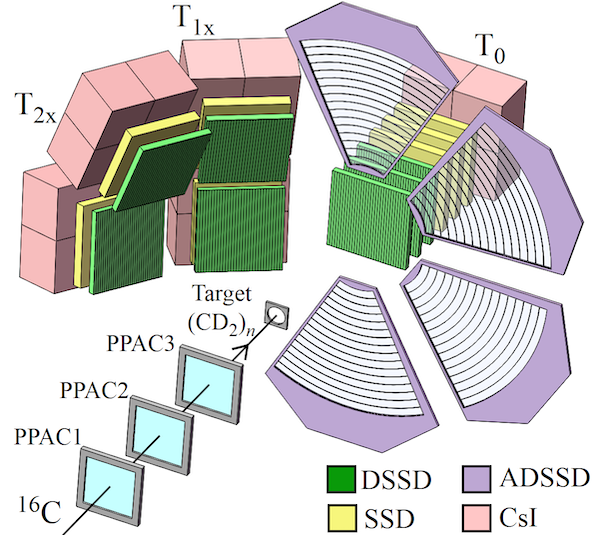
3.4 DSSD front-back correlation (I) - dssd1¶

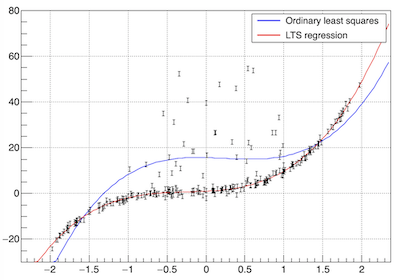
目的：¶

  1. 掌握利用正背面关联进行能量刻度的方法
  2. ROBUST fit

Front-back correlation neglecting crosstalks¶

  • 入射粒子产生的载流子在漂移过程中，在正负极上产生等量异号的感应电荷。
  • 在两侧采用不同极性的主放大器，可以得到幅度相同的正信号。
  • 即有, $E_{x_i} = E_{y_j}$

alt

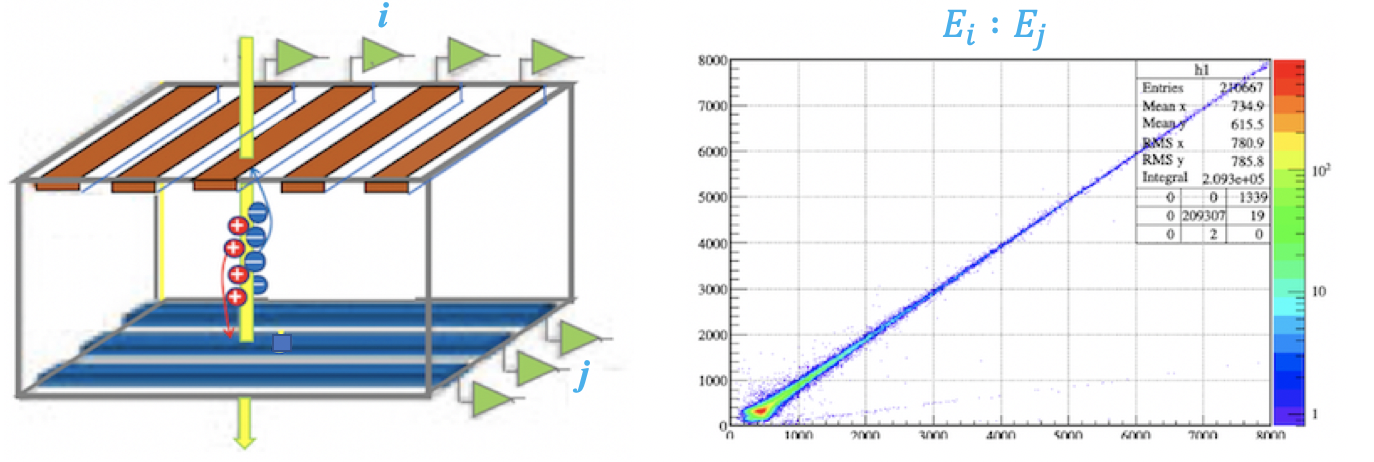
correlation¶

  • 粒子在入射位置为：xstrip = i 、ystrip = j ，标记为 $(x_i,y_j)$

  • 对于入射到 $(x_i,y_j)$ ，能量沉积为 E 的粒子, 在 x, y侧记录的信号道值分别为 $A_{x_i},A_{y_j}$:

$$ \begin{align} E_{x_i}&=k_{x_i}A_{x_i}+b_{x_i} \tag{1}\\ E_{y_j}&=k_{y_j}A_{y_j}+b_{y_j} \tag{2}\\ E&=E_{x_i}=E_{y_j} \tag{3} \end{align} $$

由(1)-(3)式可得： $$ A_{x_i}=K_{x_iy_j}A_{y_j}+B_{x_iy_j} \tag{4} $$

其中$K_{x_iy_j}=\frac{k_{y_j}}{k_{x_i}}$, $B_{x_iy_j}=\frac{b_{y_j}}{k_{x_i}} - b_{x_i}$

上式中 $K_{x_iy_j}, B_{x_iy_j}$ 称为 $A_{y_j}$ 相对于 $A_{x_i}$ 的归一化系数。

将 (4) 式与能量刻度公式 $E = k*ch +b$ 类比，可知公式(4) 给出了将 $A_{y_j}$幅度归一到$A_{x_i}$的函数关系。为方便描述，以下称 $x_i$ 为参考条， $y_j$ 为待刻度条。

上图右侧显示了$A_{x_i}与A_{y_j}$的二维关联图，可以看出二者呈现很好的线性关系，利用上式进行线性拟合即可确定$K_{x_iy_j},B_{x_iy_j}系数$。

多粒子入射位置的确定¶

  • 两个入射粒子同时入射到DSSD，实际入射位置和能量分别为：
    • 粒子1：$(x_{i_1},y_{j_1})$, $(e_{x_{i_1}}=e_{y_{j_1}})$，粒子2：$(x_{i_2},y_{j_2})$, $(e_{x_{i_2}}=e_{y_{j_2}})$, 且$(e_{x_{i_1}}\neq e_{y_{j_2}})$

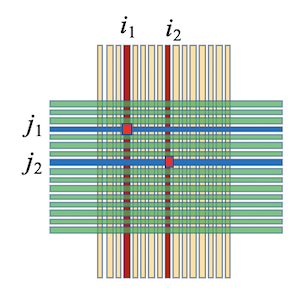
  • 可能的入射组合为$(x_{i_1},y_{j_1}),(x_{i_2},y_{j_2}) 或 (x_{i_1},y_{j_2}),(x_{i_2},y_{j_1})$

  • 与实际入射位置一致的组合，其正背面的能量差值最小，即:

    • $|e_{x_{i_1}}-e_{y_{j_1}}| < |e_{x_{i_1}}-e_{y_{j_2}}|$ && $|e_{x_{i_2}}-e_{y_{j_2}}| < |e_{x_{i_2}}-e_{y_{j_1}}|$。

  • 进行上述步骤时，必须先进行能量刻度

ROOT File : data_16C.root¶

  • Reaction: $25MeV/A \quad ^{16}C+^{9}Be$, 测量16C在靶上碎裂后的多重带电粒子产物。

  • Detector setup: 3个DSSD+CSI的望远镜阵列，放置靶后零角度方向，朝向束流。

    • D1[32x32]- D2[32x32]- D3[32x32]

      • 条宽：2mm，条间距：0.1mm

    • SSD[2]

    • CSI[2x2]

  • Geometry:

    • target:
    • $\phi=30mm$
    • z=0
    • D1:
    • z=156mm
    • D2:
    • z=176mm
    • D3:
    • z=196mm

  • Trigger: 要求D1和D2的x面，同时有两根条以上有信号( M2=Multiplicity$\ge$ 2)：

    • $D1M2 \bigotimes D2M2$

  • 事件预处理：已去除pedal事件。

Branch:¶

// xenergy, yenergy, xtime
    d1x[32], d1y[32], d1t[32]; 
    d2x[32], d2y[32], d2t[32];
    d3x[32], d3y[32], d3t[32];
//hit, energy, time, strip
    d1xhit, d1xe[d1xhit], d1xt[d1xhit], d1xs[d1xhit]; 
    d2xhit, d2xe[d2xhit], d2xt[d2xhit], d2xs[d2xhit] 
    d3xhit, d3xe[d3xhit], d3xt[d3xhit], d3xs[d3xhit]

    d1yhit, d1ye[d1yhit], d1yt[d1yhit], d1ys[d1yhit]; 
    d2yhit, d2ye[d2yhit], d2yt[d2yhit], d2ys[d2yhit] 
    d3yhit, d3ye[d3yhit], d3yt[d3yhit], d3ys[d3yhit]
In [1]:
//%jsroot on
TFile *ipf = new TFile("./data/data_16C.root");
TTree *tree = (TTree*)ipf->Get("tree");
TCanvas *c1=new TCanvas("c1","c1");

hit结构中事件已按照能量降低的顺序排序¶

In [2]:
tree->Scan("d1xe:d1xs:d1ye:d1ys","","",10,1);

***********************************************************************
*    Row   * Instance *      d1xe *      d1xs *      d1ye *      d1ys *
***********************************************************************
*        1 *        0 *      4800 *        17 *      5775 *        18 *
*        1 *        1 *       982 *        18 *           *           *
*        2 *        0 *      3069 *        23 *      3352 *        11 *
*        2 *        1 *       341 *        24 *       111 *        10 *
*        3 *        0 *      5325 *        23 *      4522 *        15 *
*        3 *        1 *           *           *       922 *        16 *
*        4 *        0 *      5822 *        21 *      5688 *        15 *
*        4 *        1 *           *           *       271 *        14 *
*        5 *        0 *      4048 *        11 *      5213 *        12 *
*        5 *        1 *      1149 *        12 *           *           *
*        6 *        0 *      3719 *        14 *      4255 *        16 *
*        6 *        1 *       374 *        13 *           *           *
*        7 *        0 *      4546 *        12 *      4961 *         9 *
*        7 *        1 *       297 *        11 *           *           *
*        8 *        0 *      4051 *        22 *      3877 *         9 *
*        8 *        1 *           *           *       329 *        10 *
*        9 *        0 *      6720 *        13 *      6513 *        12 *
*        9 *        1 *       142 *        10 *       418 *        13 *
*        9 *        2 *       109 *        14 *           *           *
*       10 *        0 *      3873 *        20 *      3007 *         8 *
*       10 *        1 *           *           *       974 *         9 *
***********************************************************************

观察x-y两侧多重性¶

  • x,y 两侧都以二重事件为主。
In [3]:
tree->Draw("d1xhit:d1yhit>>(15,0,15,15,0,15)","","colz");
gPad->SetLogz();
c1->Draw();

inter-strip correlation¶

  • 一般情况下，条间事件的比例 = 条间面积/探测器灵敏面积
  • 本实验中，由于触发的原因相邻条能量共享事件的比例大大增加。
In [4]:
tree->Draw("d1x[12]:d1x[13]>>(1000,0,8000,1000,0,8000)","","colz");//inter-strip correlation
gPad->SetLogz();
c1->Draw();
In [5]:
tree->Draw("d1x[12]>>(1000,10,1010)","","colz");
gPad->SetLogy();
c1->Draw();

front-back correlation¶

  • 由于x面和y面有相邻条之间的能量共享，可以看到中间直线区域(front-back)外有很多散点的分布。
In [6]:
gPad->SetLogy(0);
tree->Draw("d1x[12]:d1y[13]>>(1000,0,8000,1000,0,8000)","","colz");
c1->Draw();//front-back correlation

要求两侧只有一重信号¶

  • 散点减少，但统计偏少
  • 获取的条件为某一面的hit=2，因此事件中hit=1的事件很少。
    • 在前期的数据处理过程中，去掉了一些不满足时间条件的信号，导致有些x面事件的多重性由2降为1。
In [7]:
TCut chit1="d1xs==12 && d1ys==13 && d1xhit==1 && d1yhit==1";
tree->Draw("d1xe:d1ye>>(1000,0,8000,1000,0,8000)",chit1,"colz");
c1->Draw();

一重条件下，所有x条和y条正背面关联¶

  • 关联区域弥散，显示不同x-y条之间刻度系数不一致。
In [8]:
//所有x条和y条正背面关联
TCut chit = "d1xhit==1 && d1yhit==1";
tree->Draw("d1xe:d1ye>>(1000,0,8000,1000,0,8000)",chit,"colz");
gPad->SetLogz(0);
c1->Draw();

改进的关联条件¶

  • 改进的条件：不对多重性作限制，而只要求x和y面相邻条没有共享信号。

    • d1x[12]: 要求11,13条无信号共享
    • d1y[13]: 要求12,14条无信号共享

  • 应用改进关联条件后，统计显著增加。

In [9]:
TCut cveto = "d1x[11]<50 && d1x[13]<50 && d1y[12]<50 && d1y[14]<50";//no crosstalk from neighbouring strips 
TCut c1213 = "d1x[12]>200 && d1x[12]<8000 && d1y[13]>200&& d1y[13]<8000";
tree->Draw("d1x[12]:d1y[13]>>h2(1000,0,8000,1000,0,8000)", cveto&&c1213, "colz");//front-back correlation with crosstalk rejection
c1->Draw();

TH2转成TGraph进行拟合¶

In [10]:
TGraph *gr = new TGraph(tree->GetSelectedRows(), tree->GetV2(), tree->GetV1());
gr->Draw("p");//draw point
c1->Draw();

进行线性拟合¶

In [11]:
TF1 *fp1 = new TF1("fp1", "pol1", 200, 8000);
fp1->SetLineColor(kGray);
gr->Fit(fp1);
fp1->Draw();
h2->Draw("same colz");
c1->Draw();

****************************************
Minimizer is Linear / Migrad
Chi2                      =  8.70489e+08
NDf                       =          586
p0                        =      638.618   +/-   70.9968     
p1                        =     0.516471   +/-   0.0314706

拟合结果与直觉不符！¶

  • 在直线外存在大量散点(outliers, 不是由于统计涨落引起的，是由于其他机制导致的)，影响拟合结果。
  • 可以通过人为选择拟合区域(TCutG)，改善拟合。但这取决于cut范围，拟合结果随着cut范围变化而变化。

ROBUST REGRESSION¶

In the presence of outliers that do not come from the same data-generating process as the rest of the data, least squares estimation is inefficient and can be biased. Robust regression methods are designed to be not overly affected by violations of assumptions by the underlying data-generating process. common situation in which robust estimation is used occurs when the data contain outliers. https://root.cern.ch/root/html/tutorials/fit/fitLinearRobust.C.html image.png

  • ROOT 只支持多项式的Robust fitting
In [12]:
Double_t p0,p1,p2;
In [13]:
gr->Fit(fp1, "ROB");
   //The option "rob=0.75" means that we want to use robust fitting and
   //we know that at least 75% of data is good points (at least 50% of points
   //should be good to use this algorithm). If you don't specify any number
   //and just use "rob" for the option, default value of (npoints+nparameters+1)/2
   //will be taken
p0=fp1->GetParameter(0);
p1=fp1->GetParameter(1);
fp1->Draw();
h2->Draw("same colz");
c1->Draw();

****************************************
Minimizer is Linear / Robust
Chi2                      =  1.20668e+09
NDf                       =          586
p0                        =      12.9492
p1                        =     0.983987

观察残差分布¶

  • 一次多项式拟合的残差分布不是随机的。
In [14]:
TString stree;
In [15]:
stree.Form("d1y[13]:d1x[12]-(%lf*d1y[13]+%lf)>>ha(100,-50,50,1000,0,8000)", p1, p0);//%lf-Double_t
tree->Draw(stree.Data(), cveto&&c1213, "colz");//front-back correlation with crosstalk rejection
c1->Draw();//从图上看，一次函数拟合并不是很好

尝试二次多项式拟合¶

In [16]:
TF1 *fp2 = new TF1("fp2","pol2",200,8000);
gr->Fit(fp2,"ROB");//改成二次函数拟合
p0 = fp2->GetParameter(0);
p1 = fp2->GetParameter(1);
p2 = fp2->GetParameter(2);

****************************************
Minimizer is Linear / Robust
Chi2                      =  1.20693e+09
NDf                       =          585
p0                        =      10.6689
p1                        =     0.987026
p2                        = -5.43837e-07
In [17]:
fp2->SetLineColor(kGray);
fp2->Draw();
h2->Draw("colz same");
c1->Draw();
In [18]:
stree.Form("d1y[13]:d1x[12]-(%e*d1y[13]*d1y[13]+%lf*d1y[13]+%f)>>ha(100,-50,50,1000,0,8000)", p2, p1, p0);
//cout<<stree.Data()<<endl;
tree->Draw(stree.Data(), cveto&&c1213, "colz");//front-back correlation with crosstalk rejection
c1->Draw();//二次函数拟合比一次函数拟合有显著的改善。

继续调整¶

  • 目测残差分布的中心值有偏差
  • 尝试继续加条件进行拟合：限制残差范围
In [19]:
//cut proper range for fit
TCut ccut=Form("abs(d1x[12]-(%e*d1y[13]*d1y[13]+%lf*d1y[13]+%lf))<5", p2, p1, p0);
In [20]:
tree->Draw("d1x[12]:d1y[13]>>h2b(1000,0,8000,1000,0,8000)", cveto&&c1213&&ccut, "colz");
gr = new TGraph(tree->GetSelectedRows(),tree->GetV2(), tree->GetV1());
In [21]:
gr->Fit(fp2);//不用ROB选项。
p0=fp2->GetParameter(0);
p1=fp2->GetParameter(1);
p2=fp2->GetParameter(2);

****************************************
Minimizer is Linear / Migrad
Chi2                      =       710.28
NDf                       =          194
p0                        =      12.0182   +/-   0.293169    
p1                        =       0.9867   +/-   0.000363622 
p2                        = -5.14555e-07   +/-   6.61855e-08
In [22]:
stree.Form("d1y[13]:d1x[12]-(%e*d1y[13]*d1y[13]+%lf*d1y[13]+%lf)>>ha(100,-50,50,1000,0,8000)",p2,p1,p0);
tree->Draw(stree.Data(),cveto&&c1213,"colz");
c1->Draw();//比上一步有改进