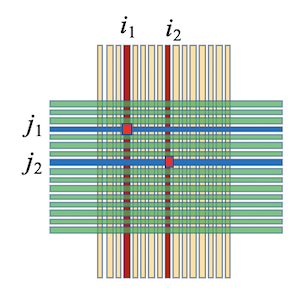
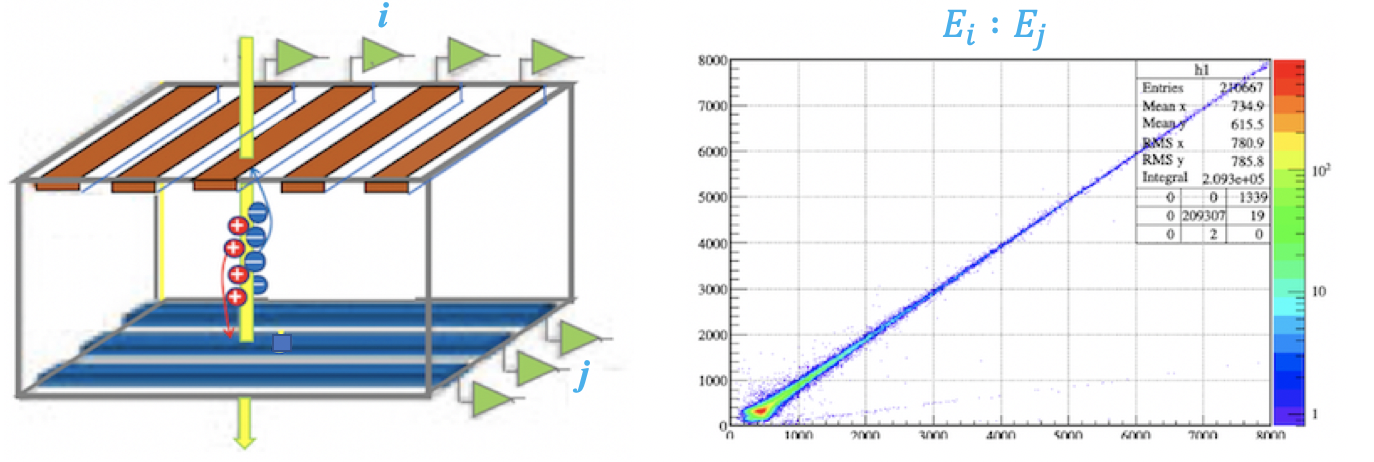
A double-sided silicon strip detector (DSSD) is used in nuclear physics to pinpoint the position and energy of incident particles. With orthogonal strip arrays on its front (x-strips) and back (y-strips), it detects charge carriers generated by a particle’s energy deposition. These carriers induce equal but opposite charges on the x- and y-strips, and amplifiers of opposite polarity produce positive signals of equal amplitude, reflecting the deposited energy.
For a particle hitting the intersection of front strip $x_i$ and back strip $y_j$, depositing energy $E$, the calibrated energy signals from both sides should match:
where $E_{xi}$ and $E_{yj}$ are the energies measured by strips $x_i$ and $y_j$.
Energy Calibration and Correlation¶
The raw signal amplitudes (channel numbers) from strips $x_i$ and $y_j$, denoted $a_{xi}$ and $a_{yj}$, relate to the deposited energy via linear calibration:
$$ E_{xi} = g_{xi} a_{xi} + o_{xi}, \tag{1} $$$$ E_{yj} = g_{yj} a_{yj} + o_{yj}, \tag{2} $$where $g_{xi}, g_{yj}$ are gain factors and $o_{xi}, o_{yj}$ are offsets. Since the deposited energy is the same ($E = E_{xi} = E_{yj}$), equating (1) and (2) gives a linear relationship between amplitudes:
$$ a_{xi} = k_{yj} a_{yj} + b_{yj}, \tag{3} $$where: $$ k_{yj} = \frac{g_{yj}}{g_{xi}}, \quad b_{yj} = \frac{o_{yj} - o_{xi}}{g_{xi}}. $$
Here, $k_{yj}$ and $b_{yj}$ are normalization coefficients that scale the amplitude $a_{yj}$ (from the "calibrated" strip $y_j$) to match $a_{xi}$ (from the "reference" strip $x_i$). A 2D plot of $a_{xi}$ vs. $a_{yj}$ shows a linear trend, and a linear fit yields $k_{yj}$ and $b_{yj}$. This calibration ensures consistent energy measurements across strips, crucial for accurate position and energy reconstruction.
Multi-Particle Position Determination¶
When two particles strike the DSSD simultaneously at positions $(x_1, y_1)$ and $(x_2, y_2)$ with distinct energies $e_1 = e_{x1} = e_{y1}$ and $e_2 = e_{x2} = e_{y2}$ ($e_1 \neq e_2$), signals are recorded from x-strips $x_1, x_2$ and y-strips $y_1, y_2$. This leads to ambiguity, as possible pairings are:
- $(x_1, y_1)$ and $(x_2, y_2)$ (correct),
- $(x_1, y_2)$ and $(x_2, y_1)$ (incorrect).
The correct pairing produces the smallest energy differences. After normalizing amplitudes using equation (3), the proper combination of $(x_1, y_1)$ and $(x_2, y_2)$ minimizes $|e_x - e_y|$ among all x- and y-strip pairings, enabling precise position reconstruction.