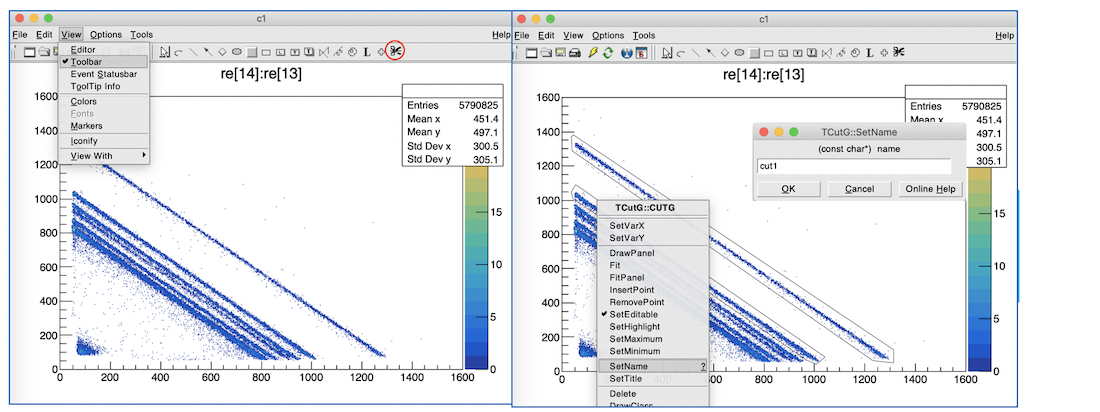
3.3 DSSD Inter-strip correlation

1. 相邻条的关联事件
2. TCutG

相邻条关联(cross-talk)

• 入射粒子入射到两条之间的缝隙，载流子被相邻两条收集，或某一条上有很大的能量沉积导致相邻条产生感应信号.

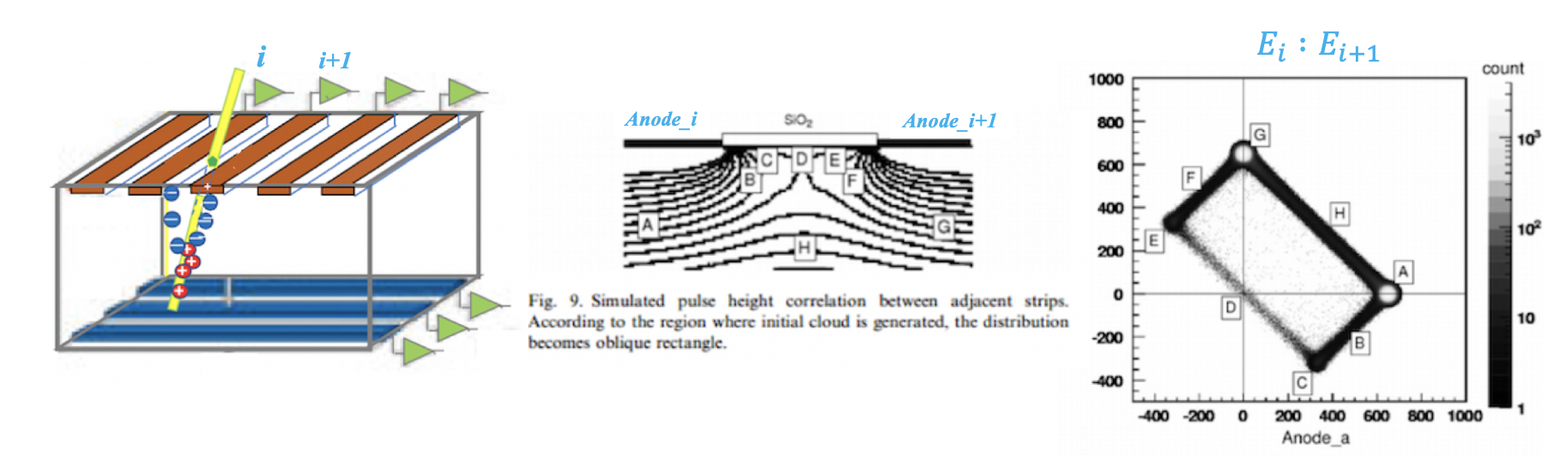
• 相邻条之间的信号关联关系与粒子的入射位置，以及入射深度都有关系，如下图(入射粒子沉积能量相同)所示。

  • 相邻条的关联在低能入射粒子（如alpha放射源）注入到浅层(BCDEF)时尤为复杂。如在B,F位置，两侧产生的的脉冲信号一正一负。
  • 当入射粒子(高能)穿过DSSD时(AHG)两侧信号都是正的。

• 一般情况下ADC只接受正脉冲信号,因此只能看见(AHG)范围内的关联，即

$E = E_i + E_{i+1}$

数据

• S4的Ring一侧，条宽很窄、条间距很小，因此相邻条之间具有显著的关联。
• 在pie条中这种关联相对不明显。

//%jsroot on
TFile *fin = new TFile("s4hit.root");
TTree *tree = (TTree*)fin->Get("tree");
TCanvas *c1 = new TCanvas;
c1->SetLogz();

Ring和pie的相邻条关联

tree->Draw("re[14]:re[13]>>hr43(800,-100,1700,800,-100,1700)","","goff");//goff 选项：只填充hist，而不显示。
tree->Draw("pe[14]:pe[13]>>hp43(800,-100,1700,800,-100,1700)","","goff");
c1->Divide(2,1);//将画布分成 2 x 1 的区域
c1->cd(1);       //进入第一个区域
hr43->Draw("colz");
c1->cd(2);       //进入第二个区域
hp43->Draw("colz");
c1->Draw();

Ring -第13条能谱

c1->Divide(1,1);
c1->cd();
tree->Draw("re[13]>>h1a(800,0,1600)","re[14]>0 || re[12]>0");// 有相邻条能量共享
TH1F *h1a = (TH1F*)gROOT->FindObject("h1a");
tree->Draw("re[13]>>h2a(800,0,1600)","re[14]<0 && re[12]<0");// 没有相邻条能量共享
h1a->SetLineColor(kRed);
h1a->Draw("same");
c1->Draw();

TCutG - 选择图形中的封闭区域作为Cut条件

• 画tree的二维关联图
• 选择Edit->Toolbar
• 在菜单栏下图形选项中选择最后一项 ✂️
• 连续点击鼠标左键选择闭合区域，双击结束
• 点击鼠标右键，选择SetName改名称(缺省为CUTG)

Write to a ROOT file

TFile *fout = new TFile("out.root","recreate");
cut1->Write();
cut2->Write();

SaveAs

root [0] cut1->SaveAs("cut1.C")
Info in <TCutG::SaveAs>: C++ Macro file: cut1.C has been generated

Load

root [1] gROOT->Macro("cut1.C"); //等价于 .x cut1.C
Info in <TCanvas::MakeDefCanvas>:  created default TCanvas with name c1

TCutG 用在不同的x:y的变量的二维图中

• 比如在

tree->Draw("re:pe");

的二维图上选择区域，存成cut.C, 打开文件cut.C，可以看到内部前几行有如下几行

cutg->SetVarX("pe");
   cutg->SetVarY("re");

当把上述TCutG 用在下面的代码时，cut不起作用。

tree->Draw("re[10]:pe[10]","cut");

原因是二维图中的x，y的变量名与cut内变量名不一致。 此时，代码应改成：

cutg->SetVarX("pe[10]");
   cutg->SetVarY("re[10]");

在代码内使用TCutG

//载入TCutG
gROOT->Macro("cut1.C");//gROOT->ProcessLine(".x cut1.C");
//获得TCutG的pointer "cut1"为SetName时指定的name
TCutG *cutg1 = (TCutG *)gROOT->GetListOfSpecials()->FindObject("cut1");
TCutG *cutg2 = (TCutG *)gROOT->GetListOfSpecials()->FindObject("cut2");
...

//判断点(x,y)是否在TCutG以内，    
bool bcut = cutg1->IsInside(Double_t x,Double_t y);//1-is inside, 0- not inside
if(bcut) {
 ...
}

!cat cut1.C

{
//========= Macro generated from object: cut1/Graph
//========= by ROOT version6.20/00
   
   TCutG *cutg = new TCutG("cut1",11);
   cutg->SetVarX("re[13]");
   cutg->SetVarY("re[14]");
   cutg->SetTitle("Graph");
   cutg->SetFillStyle(1000);
   cutg->SetPoint(0,52.149,1378.95);
   cutg->SetPoint(1,221.203,1214.74);
   cutg->SetPoint(2,430.372,1000);
   cutg->SetPoint(3,630.946,797.895);
   cutg->SetPoint(4,931.805,507.368);
   cutg->SetPoint(5,1307.16,94.7368);
   cutg->SetPoint(6,1301.43,52.6316);
   cutg->SetPoint(7,1255.59,56.8421);
   cutg->SetPoint(8,34.957,1294.74);
   cutg->SetPoint(9,37.8223,1320);
   cutg->SetPoint(10,52.149,1378.95);
   cutg->Draw("");
}

• cut1.C: 对应alpha谱中 $8.6931$ MeV
• cut2.C: 对应alpha谱中 $6.6708$ MeV

gROOT->Macro("cut1.C");
gROOT->Macro("cut2.C");

c1->Clear();
tree->Draw("re[14]:re[13]>>hcut2(800,0,1600,800,0,1600)","cut2","colz");
c1->Draw();

tree->Draw("re[14]:re[13]>>hcut1(800,0,1600,800,0,1600)","cut1","colz");
c1->Draw();

相邻条能量关联关系

$$ e_x=k_x x+b_x \quad (1)\\ e_y=k_y y+b_y \quad (2)\\ e=e_x+e_y=k_x x+ k_y y+(b_x +b_y) \quad (3)\\ $$$$ \Longrightarrow y=K x + B \quad (4) \\ K=-\frac{k_x}{k_y} , \quad B=\frac{e-(b_x+b_y)}{k_y} \quad (5) \\ $$

• 从相邻条的关联($y$-$x$), 拟合得到斜率 $K$ 和截距 $B$.

• 利用两个单能alpha$(e_1,e_2)$的相邻条关联,拟合得到$K(K_1,K_2),B_1,B_2$。

• 由公式(5)得到$k_x,k_y, b_x+b_y$, 带入(3),进行相邻条能量相加。

$$ B_1k_y=e_1-(b_{x}+b_{y}) \\ B_2k_y=e_2-(b_{x}+b_{y}) \\ k_y=\frac{e_1-e_2}{B_1-B_2} \\ k_x=-K*k_y \\ b_x+b_y=e_1-k_y*B_1 $$

二维关联图拟合

将关联数据填至TGraph进行拟合：

• 事件遍历填充TGraph
• 从tree直接转换成TGraph https://root.cern.ch/root/roottalk/roottalk03/0638.html

tree::Draw("x1:x2",selection);
TGraph *gr = new TGraph(tree->GetSelectedRows(), tree->GetV2(), tree->GetV1());

cut1( $e_1$=8.6931 $MeV$)

TGraph *gr1;
tree->Draw("re[14]:re[13]>>hcut1(800,0,1600,800,0,1600)","cut1","colz");
gr1 = new TGraph(tree->GetSelectedRows(),tree->GetV2(), tree->GetV1());
gr1->Draw("p");//draw point
gr1->Fit("pol1");
c1->Draw();

****************************************
Minimizer is Linear / Migrad
Chi2                      =       318541
NDf                       =         4747
p0                        =      1375.94   +/-   0.23085     
p1                        =     -1.01373   +/-   0.00029612  

cut2( $e_2$=$6.6708$ MeV)

TGraph *gr2;
tree->Draw("re[14]:re[13]>>hcut2(800,0,1600,800,0,1600)","cut2","colz");
gr2 = new TGraph(tree->GetSelectedRows(),tree->GetV2(), tree->GetV1());
gr2->Draw("p");//draw point
gr2->Fit("pol1");
c1->Draw();

****************************************
Minimizer is Linear / Migrad
Chi2                      =       467540
NDf                       =         7987
p0                        =      1083.65   +/-   0.164694    
p1                        =     -1.01424   +/-   0.000274002 

确定参数

double e1 = 8.6931;
double e2 = 6.6708;
double K1,K2,K,B1,B2,kx,ky,bxy;

TF1 *f1 = gr1->GetFunction("pol1");
TF1 *f2 = gr2->GetFunction("pol1");
K1 = f1->GetParameter(1);
K2 = f2->GetParameter(1);
K = (K1+K2)/2.;
B1 = f1->GetParameter(0);
B2 = f2->GetParameter(0);
ky = (e1-e2)/(B1-B2);
kx = -K * ky;
bxy = e1 - ky * B1;
cout << Form("kx=%f, ky=%f, bxy=%f",kx,ky,bxy) <<endl;

kx=0.007016, ky=0.006919, bxy=-0.826842

未刻度之前的单条能谱

tree->Draw("re[13]>>hr13(500,0,1500)","");
tree->Draw("re[14]>>hr14(500,0,1500)","");
TH1F *h1a = (TH1F*)gROOT->FindObject("hr13");
TH1F *h1b = (TH1F*)gROOT->FindObject("hr14");
h1b->SetLineColor(kRed);
h1a->Draw();
h1b->Draw("same");
c1->Draw();

刻度后相邻条能量之和

TString stree;
stree.Form("re[14]*%f+re[13]*%f+%f>>hrsum(2000,0.1,10)", ky, kx, bxy);
tree->Draw(stree.Data(),"re[13]>0 && re[14]>0","colz");
c1->Draw();

相邻条相加后事件所属的位置:

• 直接指定为能量更大的一侧的位置

• 按照能量权重计算更精确的位置:

$$ x_w=\frac{e_1 x_1+e_2 x_2}{e_1+e_2} $$