3.1 DSSD Energy Calibration

1. 能量刻度
2. TSpectrum的, vector，map
3. TH1,TGraph Fit

实验设置

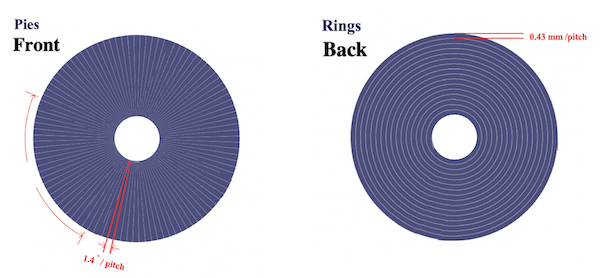
• Detectors: S4

• 128(Pie) x 128(Ring)

• Pie: $1.4^{\circ}$/条, HV=-110V

• Ring: 0.43 mm 条宽，~0.03 mm 条间距, HV=0V

• 厚度1014 $\mu$m

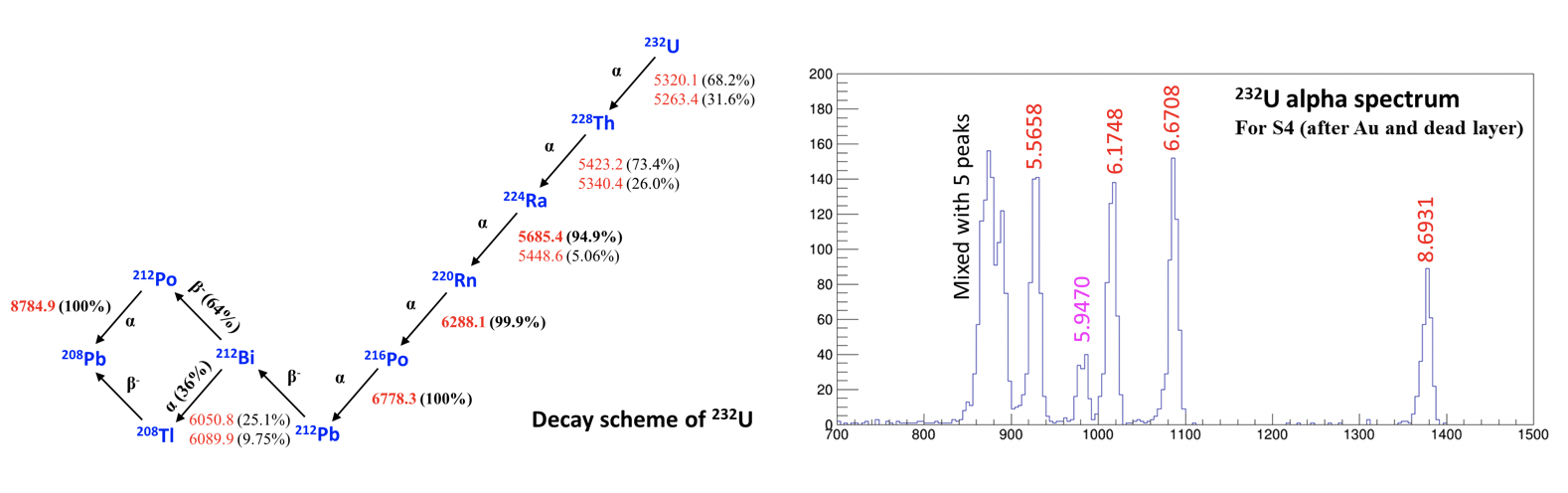
• $\alpha-$Sources: $^{232}U$

• $\alpha$粒子从Pie面入射，考虑放射源表面的金膜和Si前表面的死层后，最终沉积在Si里的能量分别为 $5.5658$ MeV, $6.1748$ MeV, $6.6708$ MeV, $8.6931$ MeV.

• 使用下图中标红色的4个峰进行刻度.

• 数据: s4.root
• 数据是用Digital modules的自触发模式记录的, 数据截取了pie和ring的前48条信息。

Int_t pe[48];//Pie 0-48
 Int_t re[48];//Ring 0-48

TFile *f = new TFile("s4.root");
TTree *tree = (TTree*)f->Get("tree");
TCanvas *c1 = new TCanvas;

tree->Draw("pe[0]>>hx0(1000, 0, 2000)");//单条
tree->Draw("pe[1]>>hx1(1000, 0, 2000)");//单条
TH1I *hx0 = (TH1I*)gROOT->FindObject("hx0");
TH1I *hx1 = (TH1I*)gROOT->FindObject("hx1");
hx0->SetLineColor(kGreen);
hx1->Draw();
hx0->Draw("same");
c1->Draw();

tree->Draw("pe>>(1000,0,2000)");//所有条pe[0-48]累积
c1->Draw();

tree->Draw("re[0]>>hy0(1000, 0, 2000)");//单条
tree->Draw("re[1]>>hy1(1000, 0, 2000)");//单条
TH1I *hy0 = (TH1I*)gROOT->FindObject("hy0");
TH1I *hy1 = (TH1I*)gROOT->FindObject("hy1");
gPad->SetLogy();
hy0->SetLineColor(kGreen);
hy1->Draw();
hy0->Draw("same");
c1->Draw();

步骤

0. 将ADC的谱进行连续化。(下列代码没做这一步)
1. 寻峰得到的 $\alpha$-峰位与已知 $\alpha$ 能量之间进行匹配(利用TSpectrum)，利用峰位估计值进行粗刻度。
2. 选取合理的拟合区间，对每个峰进行高斯拟合，得到最终刻度系数。

peaks.C --利用TSpectrum寻找histogram中的峰位，并进行标注。

• hname:待寻峰的TH1的Name；
• pe:按照峰值由高到低的顺序存储峰位
• thres:寻峰阈值
• backsub:是否减本底.

TH1F *h=NULL,*hb=NULL;
Int_t nfound;
Double_t *xpeaks=NULL, *ypeaks=NULL;
TSpectrum *s=NULL;

void peaks(TString hname, vector<Double_t> &pe, Double_t thres=0.05, int backsub=0)
{
  pe.clear();                                //清空pe
  multimap<Int_t,Double_t> me;               //用于排序, key: ypeaks, value: xpeaks
  h = (TH1F*)gROOT->FindObject(hname);
  if(!s) s = new TSpectrum(500);
  if(backsub) {
    hb = (TH1F*)s->Background(h, 80, "same"); // 80:本底光滑程度
    h->Add(h, hb, 1, -1);   
  }
  nfound = s->Search(h, 2, "", thres);       //2:gaus峰的sigma，需要根据峰的实际sigma进行调整 
  TPolyMarker *pm = (TPolyMarker *)
     h->GetListOfFunctions()->FindObject("TPolyMarker");
  pm->SetMarkerStyle(32);
  pm->SetMarkerColor(kGreen);
  pm->SetMarkerSize(0.4);
  xpeaks = s->GetPositionX();
  ypeaks = s->GetPositionY();
  TString sout;
  for(int j=0; j<nfound; j++) {
    stringstream ss;
    ss << xpeaks[j];
    TString s1 = ss.str();
    TLatex *tex = new TLatex(xpeaks[j],ypeaks[j],s1);
    me.insert(make_pair(int(ypeaks[j]),xpeaks[j]));
    tex->SetTextFont(13);
    tex->SetTextSize(14);
    tex->SetTextAlign(12);
    tex->SetTextAngle(90);
    tex->SetTextColor(kRed);
    tex->Draw();
  }
  for(auto ie = me.rbegin(); ie != me.rend(); ie++) {
    cout << ie->second << " " << ie->first <<endl;//peak,count;
    ve.push_back(ie->second);//按照计数由大到小填入
  }
  me.clear();
}

gROOT->ProcessLine(".L peaks.C");//可以在代码内部直接使用，等价于[ROOT >] .L peaks.C
vector<Double_t> pe;
Double_t e[4] = {5.5658, 6.1748, 6.6708, 8.6931};//alpha energy

peaks("hx1", pe);
gPad->SetLogy(0);
c1->Draw();

0 941 1751
1 1079 1559
2 993 1550
3 1147 1494
4 957 1359
5 1429 604
6 1047 480
7 277 239
8 1405 133

将候选峰与已知alpha峰位进行匹配

下列代码采用的策略：

• 观察能谱可知：993, 1079, 1147, 1429 为与已知alpha能量匹配的峰位。

  • 上面四个峰的高度相差不多，因此不能根据高度完全确定它们之间的前后顺序(TSpectrum寻出的峰位有时候不一定落在最高处)。
  • 当能量分辨较差时，941 和 957 可能并成一个峰。

• 观察图中峰位-alpha能量，确定匹配策略为：

  • 选择前6个峰，按照能量由大到小排序，然后取前4个峰进行匹配。
  • 匹配后用拟合的chi2/ndf进行检验。

• 更一般的策略为，将TSpectrum寻到的峰位与刻度能量进行随机组合,对比拟合后的chi2/ndf值。chi2/ndf最小的一组为匹配正确的组合。

sort(pe.begin(),pe.begin()+6); 
Double_t mpe[4], cpe[4];//peak,count
for(int i=0; i<4; i++) {
    mpe[i] = pe[2+i];
    cpe[i] = hx1->GetBinContent(hx1->FindBin(mpe[i]));
    cout << mpe[i] << " " << cpe[i] << endl;
}

993 1550
1079 1559
1147 1494
1429 604

拟合确认，峰的匹配是否正确

TGraph *gr = new TGraph(4, mpe, e);
gr->Draw("A*");
gr->Fit("pol1");
TF1 *f1 = gr->GetFunction("pol1");
c1->Draw();

****************************************
Minimizer is Linear / Migrad
Chi2                      =  4.40562e-05
NDf                       =            2
p0                        =     -1.56557   +/-   0.0168397   
p1                        =   0.00717874   +/-   1.43506e-05 

通过残差图评估拟合结果

How can I tell if a model fits my data?

• a small $\chi^2$ value does not guarantee that the model fits the data well. Use of a model that does not fit the data well cannot provide good answers to the underlying engineering or scientific questions under investigation.

• Residual: $e_i=y_i-f(x_i|\alpha)$

• Residual Plot: When conducting a residual analysis, a "residuals versus fits plot" is the most frequently created plot. It is a scatter plot of residuals on the y axis and fitted values (estimated responses) on the x axis. The plot is used to detect non-linearity, unequal error variances, and outliers.

• If the model fit to the data were correct, the residuals would approximate the random errors that make the relationship between the explanatory variables and the response variable a statistical relationship. Therefore, if the residuals appear to behave randomly, it suggests that the model fits the data well. On the other hand, if non-random structure is evident in the residuals, it is a clear sign that the model fits the data poorly.

• Fig a. This plot looks good in that the variance is roughly the same all the way across and there are no worrisome patterns. There seems to be no difficulties with the model or data.

• Fig b. This plot shows two difficulties. First, the pattern is curved which indicates that the wrong type of model was used. Second, the variance (vertical spread) increases as the fitted values (predicted values) increase.

• Fig c.This plot shows that the residual variance (vertical spread) increases as the fitted values increase. This violates the assumption of constant error variance.

Double_t p0 = f1->GetParameter(0);
Double_t p1 = f1->GetParameter(1);
Double_t dpe[4];
for(int i=0; i<4; i++) 
    dpe[i] = p0 + p1 * mpe[i] - e[i];
TGraph *rgr = new TGraph(4,mpe,dpe);
rgr->Draw("A*");
c1->Draw();

确定拟合区间，进行高斯拟合

• 设定合理的拟合初值，进行拟合
• 峰位，峰高用前面得到的数据，半高宽直接目测估计。
• alpha峰位低能部分不对称，拟合区域偏向峰位高能部分

hx1->Draw();
c1->Draw();

double par[4][3];//peak,sigma,chi2/ndf
double ge[4];
TF1 *fg[4];
TFitResultPtr fr;
for(int i=0; i<4; i++) {
    fg[i] = new TF1(Form("fg%d", i), "gaus");
    fg[i]->SetParameters(cpe[i], mpe[i], 4);//constant,mean, sigma
    fr = hx1->Fit(fg[i], "SQ+", "", mpe[i]-5, mpe[i]+8);//superimpose TF1 to hx1
    par[i][0] = fg[i]->GetParameter(1);
    par[i][1] = fg[i]->GetParameter(2);
    par[i][2] = fr->Chi2()/fr->Ndf();
    ge[i] = par[i][0];
    cout << Form("peaks = %4.1f, sigma = %.2f, chi2/ndf = %.2f", 
                 par[i][0], par[i][1], par[i][2]) << endl;
}
c1->Draw();

peaks = 992.9, sigma = 3.98, chi2/ndf = 12.91
peaks = 1078.3, sigma = 4.00, chi2/ndf = 11.31
peaks = 1147.3, sigma = 3.98, chi2/ndf = 13.35
peaks = 1429.0, sigma = 4.83, chi2/ndf = 1.27

TGraph *gr1 = new TGraph(4,ge,e);
gr1->Draw("A*");
gr1->Fit("pol1");
TF1 *f2 = gr->GetFunction("pol1");
c1->Draw();

****************************************
Minimizer is Linear / Migrad
Chi2                      =  5.94348e-06
NDf                       =            2
p0                        =     -1.55862   +/-   0.00618008  
p1                        =   0.00717354   +/-   5.26708e-06 

p0 = f2->GetParameter(0);
p1 = f1->GetParameter(1);
for(int i=0; i<4; i++) 
    dpe[i] = p0 + p1 * ge[i] - e[i];
TGraph *rgr1 = new TGraph(4, ge, dpe);
rgr1->Draw("A*");
c1->Draw();

tree->Draw(Form("pe[0]*%f+%f>>hx1e(1000, -1, 10)", p1, p0));//单条
hx1e->Draw();
c1->Draw();//存在锯齿，需要在刻度前进行连续化。