2.1 PPAC 信号处理-I¶

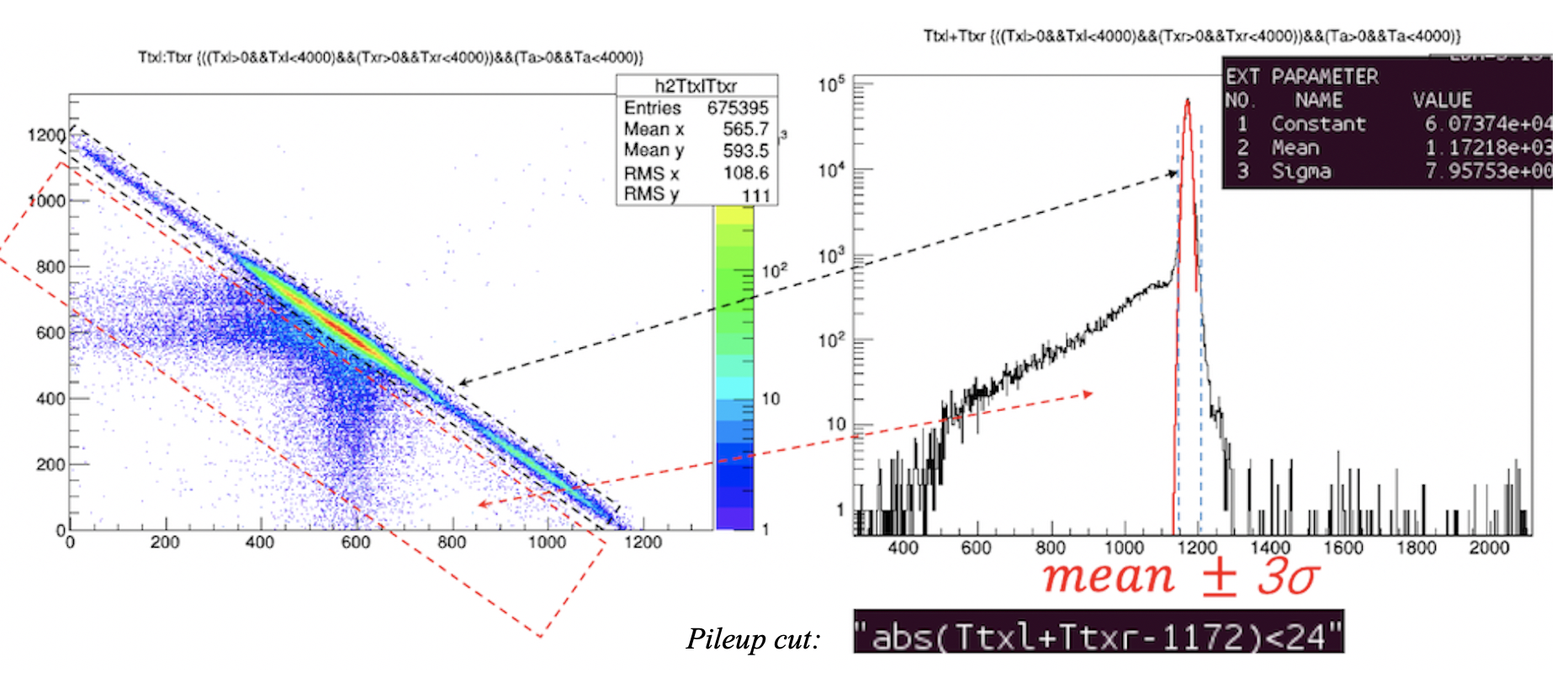
实验设置:¶

实验中，F8PPAC1-3测量靶前束流的入射方向。靶后两套望远镜系统(MUST2)测量反应产生的轻粒子，剩余重核由零度磁谱仪(ZDS)探测。为了减少散射粒子在靶内的能量损失，把靶框旋转45° 朝向望远镜摆放。靶前放置了厚铁块组成的屏蔽体，避免束流中偏离中心线的粒子达到靶后的探测系统。

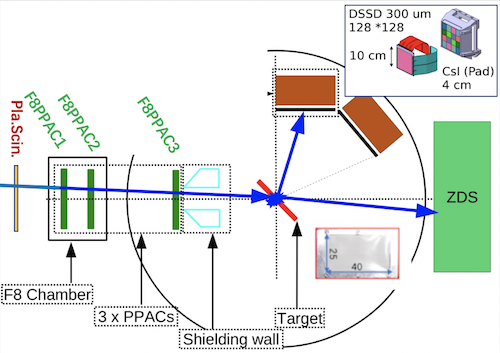
setup

Delayline PPAC 信号定义:¶

  • $T_{delay}$: 信号在延迟线的总传播时间
  • 粒子在(x,y)位置穿过PPAC。原始电离产生的电子向阳极漂移过程中产生雪崩，在阳极以及X，Y阴极产生感应信号。
  • 阳极为一整块薄镀铝mylar膜,阳极时间信号$t_a$ 作为信号到达PPAC的时间。
  • 阴极分成1mm间隔的读数条(strips),每条之间通过延迟线连接。信号沿延迟线的两端传输，通过延迟线两端时间差给出x和y方向的位置。
  • 噪声干扰等可以在x或y的两端产生时间信号。为了避免上述干扰，一般要求x，y的两端信号和阳极信号有符合关系。

PPAC

$$ \begin{align} &T_{delay} = t_{x_1}+t_{x_2} \\ &t_{x_1}= (\frac{L}{2}+x )\frac{T_{delay}}{L} \\ &t_{x_2}= (\frac{L}{2}-x )\frac{T_{delay}}{L} \\ &x=(t_{x_2}-t_{x_1})\frac{L}{2T_{delay}} \end{align} $$

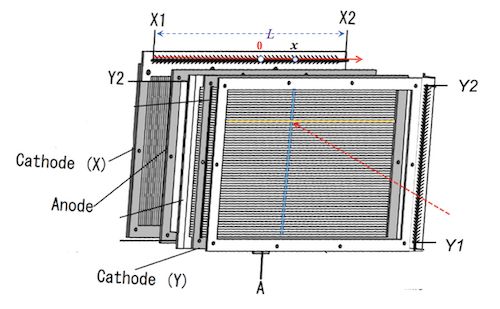
PPAC postion calibration¶

  • 将$\alpha$-放射源置于远处, $\alpha$粒子入射到盖有Mask的探测器上(Mask上孔的位置分布已知), 得到x方向和y方向的一系列峰位。通过拟合时间差谱的峰位和实际位置，得到系数$k$(=$L/T_{delay}$).
  • 探测器安装到束流线后，通过位置测量，确定探测器中心相对于束流中心线的偏移b。
  • 实验中，测量通过中心线的束流(限制束流线上的slit(狭缝)的位置)的位置，进一步检验和校准上述偏移。

TDC

两种类型PPAC:¶

实验中采用了两种不同规格尺寸的 PPAC¶

  • 一种是double PPAC(F8PPAC1, F8PPAC2), 面积为 $240 × 150 mm^2$
  • 另一种是single PPAC(F8PPAC3), 面积为 $100 × 100 mm^2$。

setup

文件中TreeBranch的定义:¶

  • Trigger = beamTrig + must2Trig

    • beamTrig=1，由靶前plastic scin.探测器触发(束流的取样触发)。
    • must2Trig=1，由靶后Must2望远镜信号触发

  • F8PPACRawData[i][j] -Raw Data(原始信息，道值)

Branch PPAC
F8PPACRawData[0][0] PPAC 1 Layer A $T_{x1}$
F8PPACRawData[0][1] PPAC 1 Layer A $T_{x2}$
F8PPACRawData[0][2] PPAC 1 Layer A $T_{y1}$
F8PPACRawData[0][3] PPAC 1 Layer A $T_{y2}$
F8PPACRawData[0][4] PPAC 1 Layer A $T_a$
F8PPACRawData[1][0-4] PPAC 1 Layer B
F8PPACRawData[2][0-4] PPAC 2 Layer A
F8PPACRawData[3][0-4] PPAC 2 Layer B
F8PPACRawData[4][0-4] PPAC 3

PPAC 信号分析¶

  • Trigger(time start): Plastic scintillator
  • 飞行距离 D：plastic to PPAC
  • 阴极，阳极信号的offset: $t_{o_1}，t_{o_2}，t_{o_a}$
  • TDC记录的时间信号：$T_{x_1}，T_{x_2}，T_a$

阴极时间 ($v$-dependence)¶

  • $ T_{x_1}=D/v+t_{x_1}+t_{o_1} $

  • $ T_{x_2}=D/v+t_{x_2}+t_{o_2} $

  • $ T_{x_1}+T_{x_2}=2D/v+T_{delay}+(t_{o_1}+t_{o_1})$

  • $T_{x_1}-T_{x_2}=t_{x_1}-t_{x_2}+(t_{o_1}-t_{o_2})$

阳极时间¶

  • $T_{a}=D/v+t_{o_a}$

组合参数 (no $v$-dependence)¶

上述时间信号不仅与感应信号在探测器中的传输时间相关，也与束流的到达时间(飞行时间)有关。 研究探测器的信号特征时，我们希望得到只和探测器性能有关的参数，此时参数的变化规律只与探测器特性有关，与束流的到达时间无关。

  • $ dt_{x_1}=T_{x_1}-T_a=t_{x_1}+(t_{o_1}+t_{o_a})$

  • $dt_{x_2}=T_{x_2}-T_a=t_{x_2}+(t_{o_2}+t_{o_a})$

  • $dt_{x_1}-dt_{x_1}=t_{x_1}-t_{x_2}+(t_{o_1}-t_{o_2})$

  • $dt_{x_1}+dt_{x_2}=t_{x_1}+t_{x_2}+(t_{o_1}+t_{o_2}-2t_{o_a})$=Const.

In [1]:
//%jsroot on
TFile *ipf = new TFile("f8ppac001.root");//  $HOME/data/MUST2@BigRIPS/ROOTFILE/
TTree *tree = (TTree*) ipf->Get("tree");
TCanvas *c1 = new TCanvas("c1","c1");
In [2]:
tree->Draw("F8PPACRawData[0][0]>>hx1(1000,0,4200)");//F8PPAC1A-Tx1
tree->Draw("F8PPACRawData[0][1]>>hx2(1000,0,4200)");//F8PPAC1A-Tx2
TH1D *hx1 = (TH1D*)gROOT->FindObject("hx1");
TH1D *hx2 = (TH1D*)gROOT->FindObject("hx2");
hx1->SetLineColor(kBlue);
hx2->SetLineColor(kBlack);
hx1->Draw();
hx2->Draw("same");
c1->SetLogy();
c1->Draw();
In [3]:
tree->Draw("F8PPACRawData[0][2]>>hy1(1000,0,4200)");//F8PPAC1A-Ty1
tree->Draw("F8PPACRawData[0][3]>>hy2(1000,0,4200)");//F8PPAC1A-Ty2
TH1D *hy1 = (TH1D*)gROOT->FindObject("hy1");
TH1D *hy2 = (TH1D*)gROOT->FindObject("hy2");
hy1->SetLineColor(kBlue);
hy2->SetLineColor(kBlack);
hy1->Draw();
hy2->Draw("same");
c1->SetLogy();
c1->Draw();
In [4]:
tree->Draw("F8PPACRawData[0][4]>>ha(1000,0,4200)");//F8PPAC1A-Ta
ha->Draw();
c1->Draw();

选取时间信号的范围¶

  • x1,x2：0-4000
  • y1,y2: 0-4000
  • anode: 0-4000
  • 每个位置信号都需要有符合的阳极信号。
  • 上述范围外的时间信号为偶然符合或异常信号。
In [5]:
TCut ca = "Ta>0 && Ta<4000";
TCut cx1 = "Tx1>0 && Tx1<4000" && ca;
TCut cx2 = "Tx2>0 && Tx2<4000" && ca;
TCut cy1 = "Ty1>0 && Ty1<4000" && ca;
TCut cy2 = "Ty2>0 && Ty2<4000" && ca;

TCut cppac=cx1 && cx2 && cy1 && cy2;
In [6]:
// F8PPAC
tree->SetAlias("Tx1", "F8PPACRawData[0][0]");//F8PPAC1A-txl
tree->SetAlias("Tx2", "F8PPACRawData[0][1]");//F8PPAC1A-txr
tree->SetAlias("Ty1", "F8PPACRawData[0][2]");//F8PPAC1A-tyu
tree->SetAlias("Ty2", "F8PPACRawData[0][3]");//F8PPAC1A-tyd
tree->SetAlias("Ta", "F8PPACRawData[0][4]");//F8PPAC1A-Anode

tree->SetAlias("dtx1", "Tx1-Ta");
tree->SetAlias("dtx2", "Tx2-Ta");
tree->SetAlias("dty1", "Ty1-Ta");
tree->SetAlias("dty2", "Ty2-Ta");

tree->Draw(“valexpr”,"selection", "option")的“selection”：¶

  • TCut条件不加 “ ”:tree->Draw("dtx1>>hdx1(2000,-4000,4000)", cx1 );
  • 变量表达式加“ ” : tree->Draw("dtx1>>hdx1(2000,-4000,4000)", cx1 && "Tx1>0" );
In [7]:
tree->Draw("dtx1>>hdx1(2000,-4000,4000)",cx1); 
tree->Draw("dtx2>>hdx2(2000,-4000,4000)",cx2);
TH1D *hdx1 = (TH1D*)gROOT->FindObject("hdx1");
TH1D *hdx2 = (TH1D*)gROOT->FindObject("hdx2");
hdx1->SetLineColor(kBlue);
hdx2->SetLineColor(kBlack);
hdx1->Draw();
hdx2->Draw("same");
c1->SetLogy();
c1->Draw();
c1->Draw();
In [8]:
tree->Draw("dtx1-dtx2>>(2000,-4000,4000)",cx1 && cx2);
c1->SetLogy();
c1->Draw();

探测器两端信号关联¶

  • $ T_{x_1}+T_{x_2}=2D/v+T_{delay}+(t_{o_1}+t_{o_1})$=$2D/v+Const.$ - 与束流速度有关

  • $dt_{x_1}+dt_{x_2}=t_{x_1}+t_{x_2}+(t_{o_1}+t_{o_2}-2t_{o_a})$=$Const.$ - 与束流速度无关

In [9]:
tree->Draw("Tx1:Tx2>>(1000,0,2500,1000,0,2500)",cx1 && cx1,"colz");
gStyle->SetPalette(1);
c1->SetLogy(0);
c1->Draw();
In [10]:
tree->Draw("dtx1:dtx2>>(1000,-100,1500,1000,-100,1500)",cx1 && cx2 && ca,"colz");
gStyle->SetPalette(1);
c1->Draw();

Pileup Cut¶

在束流强度较大时，需要考虑堆积(Pileup)事件的排除。

  • 当同时有2个或以上的粒子打在 PPAC 上时，到达 delayline 的 x 的两端的时间由不同粒子的信号给出。

    • 假设 a, b 粒子同时穿过探测器, 且 a 粒子靠近 x$_1$ 侧, b 粒子靠近 x$_2$ 侧，则$T_{x_1}$由a粒子给出, $T_{x_2}$ 则有 b 粒给出。

    (TDC 只记录与 start 信号最近的第一个信号)。

  • 此时，$T_{x_1}+T_{x_2} < T_{delay}$。即 delayline 的两端信号传输时间和不再是常数。这个条件可作为信号堆积的标志。

  • 从上述讨论可知，PPAC 无堆积条件：前后两个粒子到达探测器的时间间隔大于 $T_{delay}$

multihit

fit sum-peak¶

In [11]:
tree->Draw("dtx1+dtx2>>hdxt(1200,400,1600)",cx1 && cx2 && ca);
hdxt->Fit("gaus","","",1130,1200);
gPad->SetLogy();
hdxt->Draw();
c1->Draw();

 FCN=21486 FROM MIGRAD    STATUS=CONVERGED      86 CALLS          87 TOTAL
                     EDM=4.11835e-11    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     3.03545e+04   5.47631e+01   2.79199e+00   3.33928e-08
   2  Mean         1.17219e+03   1.02827e-02   7.33299e-04   3.35781e-04
   3  Sigma        7.95989e+00   1.01087e-02   2.01749e-05  -1.84311e-02
In [12]:
TF1 *fx = hdxt->GetFunction("gaus");
Double_t xpeak = fx->GetParameter(1);
Double_t xsigma = fx->GetParameter(2);
cout << xpeak + 3*xsigma << endl;

1196.07
In [13]:
tree->Draw("dty1+dty2>>hdyt(1200,0,1200)",cy1 && cy2 && ca);
hdyt->Fit("gaus","","",600,680);
gPad->SetLogy();
hdyt->Draw();
c1->Draw();

 FCN=22514.9 FROM MIGRAD    STATUS=CONVERGED      66 CALLS          67 TOTAL
                     EDM=4.06657e-11    STRATEGY= 1  ERROR MATRIX UNCERTAINTY   2.2 per cent
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     2.71081e+04   4.89719e+01  -8.59851e-03  -1.21529e-07
   2  Mean         6.61670e+02   1.21740e-02   7.22800e-06   8.53369e-04
   3  Sigma        8.43106e+00   1.15025e-02  -1.17691e-07  -2.94895e-02
In [14]:
TF1 *fy = hdyt->GetFunction("gaus");
Double_t ypeak = fy->GetParameter(1);
Double_t ysigma = fy->GetParameter(2);

pile-up rejection condition¶

In [15]:
TString spileup;
spileup.Form("abs(dtx1+dtx2-%f)<3*%f",xpeak,xsigma);
TCut cxpileup = spileup.Data();
spileup.Form("abs(dty1+dty2-%f)<3*%f",ypeak,ysigma);
TCut cypileup = spileup.Data();
TCut cpileup = cxpileup && cypileup;

检验探测器参数之间的关系¶

  • $ T_{x_1}+T_{x_2}=2D/v+T_{delay}+(t_{o_1}+t_{o_2})$
  • $T_{a}=D/v+t_{o_a}$
In [16]:
tree->Draw("(Tx1+Tx2)/2:Ta>>(100,250,550,200,400,1400)",cppac,"colz");
gPad->SetLogy(0);
gPad->SetLogz();
c1->Draw();
In [17]:
tree->Draw("(Tx1+Tx2)/2:Ta>>(100,250,550,200,400,1400)",cppac&&cpileup,"colz");
gPad->SetLogy(0);
gPad->SetLogz();
c1->Draw();

PPAC x-y分布¶

In [18]:
tree->Draw("dty1-dty2:dtx1-dtx2",cppac && cpileup,"colz");
gPad->SetLogy(0);
c1->Draw();