1.3 ADC,TDC信号处理¶

  • 学习处理ADC、TDC记录的信号的处理方法

实验设置：中子飞行时间谱测量（参照1.1描述）¶

物理过程¶

  • 束流轰击靶以产生带电粒子、n、$\gamma$等粒子,重带电粒子碎片被靶后 Dipole magnet偏走，而部分轻带电粒子(LP: light particles，主要为质子)没有被完全偏走，仍然进入中子探测器。

获取系统触发¶

  • DAQ的触发(Trigger)由两部分构成。主触发 (Trig$_{M}$) 由靶前塑料闪烁体探测器和靶后中子探测器符合信号产生; 另外为了监测束流，通常将靶前塑料闪烁体信号按一定比例分除作为束流触发 (Trig$_{beam}$) 加入到触发中(参见实验方法的获取部分)。获取系统触发 Trigger 为两个触发的或信号，即 Trigger = Trig$_{M}$ + Trig$_{beam}$ , Trigger信号经过适当的处理(延迟+展宽)，作为ADC的Gate和TDC的start信号。

事件标记¶

  • ROOT文件中，由 Trig$_{M}$ 触发的事件，按粒子种类标记为 $\gamma$: pid=0; neutron: pid=1; LP: pid=2。其余的事件，即由 Trig$_{beam}$ 触发的事件记为pid=3，此类事件在中子探测器上不产生信号。

  • 不同类型事件的比例为

    • $\gamma$: RatioGamma
    • neutron: RatioNeutron
    • LP: RatioLP
    • 其余: 1-RatioGamma-RatioNeutron-RatioLP

ADC & TDC¶

  • ADC将输入信号的幅度转换成数字信号。VME ADC 输入信号幅度范围一般为0-4V, 经 AD 转换后，记录为 0-4095 (12-bit插件) 范围的整数, 其数值称为道值(channel)，每道对应幅度为 LSB = 4000/4095 $\approx$ 1 mV。当输入信号幅度超过最大范围时(称为超界，overflow)，ADC 将其记录为最高道值 4095 (取决于 ADC 的具体数据格式，有些 12-bit ADC 记为 8191 道)。

  • TDC 记录 stop 信号 t$_{stop}$ 和 start 信号 t$_{start}$ 的差值 $\Delta$ t = t$_{stop}$-t$_{start}$。对于12位 TDC，当量程为 $\Delta $ T =200 ns时, LSB = 200/4095 $\approx$ 50 ps。 当$\Delta$ t > $\Delta$ T, 或无 stop 信号(超界)，TDC 将其记录为 4095 道(取决于 TDC 的具体数据格式，有些 12-bit TDC 记为 8191 道)。

  • 对于 12-bit 的 ADC 和 TDC ，当使用 sliding scale 技术来减少信号的非线性时，只有 0-3840 ch 范围的数据是准确的。3841-4095 ch范围的数据不再准确。另外，一般来说 ADC 和 TDC 在道值较低的时候线性不太好。使用时要注意上述特性，通过选择合适放大倍数，使信号幅度位于上述动态范围区间。

Pedestal¶

  • ADC 在 Gate 的宽度范围内寻找输入信号的最大幅度（如下图所示)，将其转换成道值。当 Gate 范围内没有实际信号时，ADC 将记录 Gate 宽度内基线噪声的最大值。基线噪声幅度服从高斯分布。Gaus 峰的中心值为基线的平均幅度，Gaus 峰的$\sigma$值表示随机噪声的涨落范围，上述两个数值分别记为V$_{base}，\sigma_{noise}$。

  • 常用的 ADC 一般只能记录输入信号的正幅度。当输入信号基线电平为负值 (如 -50 mV) 时, 为避免小信号(如脉冲幅度< 50 mV)不能被正常记录，ADC叠加一个正电平(由用户设置，如 V$_{ADCbase}=200 道$)叠加到输入信号上。此时ADC记录的信号基线平均道值为 V$_{base}$ + V$_{ADCbase}$，称为 Pedestal 值，简称 pedal 值。因此 ADC 记录到的实际脉冲幅度 = ADC 道值 - pedal。一般取 pedal + 3 $\sigma_{noise}$ 作为噪声和正常信号的界限。

  • Zero-Supression/Overflow-Supression：

    • 为了减少插件到后端计算机之间传输数据量 (数据传输时间是 DAQ 死时间的主要来源)，获取中将 ADC 的道值低于pedal + 3 $\sigma_{noise}$ 的事件舍弃 (zero-supression)，不传输。类似地，TDC 在传输前将超界信号舍弃 (Overflow supression).

  • 实验中观察 pedal 峰位和宽度随着时间的变化，可以得知探测器和电子学有无异常，以及异常出现的时间。因此在获取系统死时间不大的情况下，最好不用zero-supression模式。如果在实验中使用 zero-supression 模式传输数据时，应在实验前和实验后测量 pedestal 峰的位置以及宽度。

ADC/QDC Gate_Signal & Pedestal peak¶

1

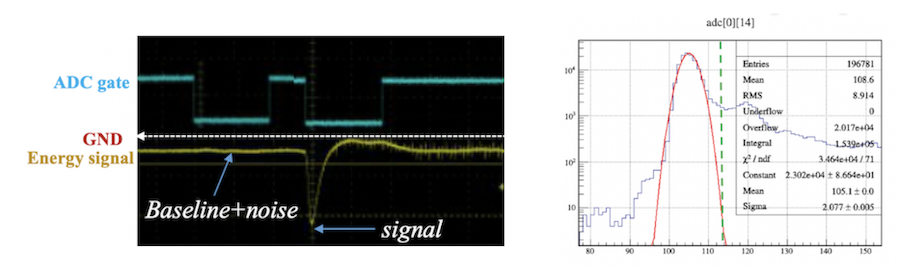
  • 实验中通过调节每个探测器的放大倍数、信号的时间延迟，将感兴趣的信号调到 ADC 和 TDC 的量程范围之内，这里gamma和中子事件是我们感兴趣的事件。其他不感兴趣的信号，如轻带电粒子信号则不要求一定在量程范围内。

  • TDC的超界信号为无效信号；ADC的低于噪声阈值之下的信号为无效信号，ADC超界信号虽然不知道实际的幅度大小，但仍具有一定意义(即为某种大信号)。

代码说明¶

通过调节电子学，使中子和 gamma 的大部分事件的时间和能量，落在TDC，ADC的量程范围内；pid=3 的事件在 ADC 的 Gate 范围内无实际物理信号 (pedal)，在TDC的量程范围内没有stop信号。

// 将下列代码保存到treeADC.cc
// 在ROOT环境中运行：
// .x treeADC.cc
// 生成 treeADC.root 文件

void treeADC()
{
  const Double_t D = 500.;//cm, distance between target and the scin.(Center)
  const Double_t L = 100.;//cm, half length of the scin.
  const Double_t dD = 5.;//cm, thickness of the scin.
  const Double_t tRes = 1.;//ns, time resolution(FWHM) of the scintillator.
  const Double_t Lambda = 380.;//cm, attenuation lenght of the scin.
  const Double_t qRes = 0.1;//relative energy resolution(FWHM) of the scin. 
  const Double_t Vsc = 7.5;//ns/cm, speed of light in the scin.
 //neutron & gamma
  const Double_t En0 = 50;//MeV, average neutron energy
  const Double_t EnFWHM = 50.;//MeV, energy spread of neutron(FWHM)
  const Double_t Eg0 = 10;//MeV, gamma energy  

  const Double_t RatioNeutron = 0.75;//ratio of neutron 
  const Double_t RatioGamma = 0.05;//ratio of gamma; 

  //charged particle hited in Neutron Detector, 
  const Double_t RatioLP = 0.1;//ratio of LP
  const Double_t Elp0 = 50;//MeV
  const Double_t ElpFWHM = 50;//MeV energy spread of LP(FWHM)

  //ADC
  const Double_t ADCuGain = 40;//1MeV=40ch.
  const Double_t ADCdGain = 45;
  const Double_t ADCuPed = 140;//baseline of ADC for upper side
  const Double_t ADCdPed = 130;//                for bottom side
  const Double_t ADCnoise = 10;//sigma of noise
  const Int_t    ADCoverflow = 4095;

  //TDC
  const Double_t TriggerDelay = 15;//ns, trigger延迟,将感兴趣的时间信号放在TDC量程以内。
  const Double_t TDCuCh2ns = 25.;//1ns=25ch.
  const Double_t TDCdCh2ns = 28.;
  const Int_t TDCoverflow = 4095;

  TFile *opf = new TFile("treeADC.root","recreate");//新文件tree.root的指针 *opf
  TTree *opt = new TTree("tree","tree structure");//新tree的指针 *opt

  // 定义tree的branch变量
  Double_t x;
  Double_t e;
  int pid;    //0/1/2/3: gamma/neutron/LP/No_particle
  Double_t tof, ctof;
  Double_t tu, td;
  Double_t qu, qd;
  Int_t itu, itd;//TDC
  Int_t iqu, iqd;//ADC

  Double_t diff;


  Double_t tuoff = 5.5;//time offset
  Double_t tdoff = 20.4;//time offset

  // 将变量分支添加到tree结构中,第一个参数为变量名称，第二个为上面定义的变量地址，第三个为变量的类型说明，D表示Double_t。
  opt->Branch("x", &x, "x/D");//position
  opt->Branch("e", &e, "e/D");//energy
  opt->Branch("tof", &tof, "tof/D");//time of flight
  opt->Branch("ctof",&ctof,"ctof/D");//TOF from exp. data
  opt->Branch("pid", &pid, "pid/I");
  // raw time and energy
  opt->Branch("tu", &tu, "tu/D");
  opt->Branch("td", &td, "td/D");
  opt->Branch("qu", &qu, "qu/D");
  opt->Branch("qd", &qd, "qd/D");

  // energy in ADC, time in TDC 注意，以下Branch变量声明的类型为 Integer，
  opt->Branch("itu", &itu, "itu/I");
  opt->Branch("itd", &itd, "itd/I");
  opt->Branch("iqu", &iqu, "iqu/I");
  opt->Branch("iqd", &iqd, "iqd/I");

  opt->Branch("diff",&diff,"diff/D");


  TRandom3 *gr=new TRandom3(0);
  // 循环，逐事件往tree结构里添加对应分支信息。
  for(int i = 0 ; i < 1000000 ; i++){
    x = gr->Uniform(-L, L);
    Double_t Dr = D + gr->Uniform(-0.5, 0.5) * dD;
    Double_t d = TMath::Sqrt(Dr * Dr + x * x);//cm, flight path

    //pid
    pid = -1;

    Double_t ratio = gr->Uniform();
    if(ratio < RatioGamma) 
        pid = 0;
    if(ratio >= RatioGamma && ratio < RatioGamma + RatioNeutron) 
        pid = 1;
    if(ratio >= RatioGamma + RatioNeutron 
        && ratio < RatioGamma + RatioNeutron + RatioLP) 
        pid = 2;
    if(ratio >= RatioGamma + RatioNeutron + RatioLP) 
        pid = 3;

    // energy & tof    
    if(pid == 0) {//gamma
       e = Eg0;
       tof = 3.333 * (d * 0.01);
      }
    if(pid == 1) { //neutron
       e = gr->Gaus(En0, EnFWHM/2.35); // neutron
       tof = 72.29824/TMath::Sqrt(e) * (d * 0.01);//ns
    }
    if(pid == 2) {//LP
      e = gr->Gaus(Elp0, ElpFWHM/2.35); // LP
      tof = 72.29824/TMath::Sqrt(e) * (d * 0.01);
    }
    if(pid == 3) {
      e = -1;
      tof = -1;
    }

    if(pid < 0 || isnan(tof)) continue; //check ZeroDivisionError

    if(pid == 3) {
      tu = -1;
      td = -1;
      qu = -1;
      qd = -1;
    }
    else {
      //time
      tu = tof + (L - x)/Vsc + tuoff - TriggerDelay;
      td = tof + (L + x)/Vsc + tdoff - TriggerDelay;
      //resolution
      tu += gr->Gaus(0, tRes/2.35); 
      td += gr->Gaus(0, tRes/2.35); 

     //energy
      Double_t Q0;
      if(pid != 2) Q0 = e * gr->Uniform();//neutron & gamma,
      else Q0 = e ; //charged particle，full energy。

      //resolution
      Q0=gr->Gaus(Q0, Q0*qRes/2.35);      

      //light transmission within the plastic
      qu = Q0 * TMath::Exp(-(L-x)/Lambda);
      qd = Q0 * TMath::Exp(-(L+x)/Lambda); 
    }


    //TDC, ADC
    if(pid == 3) {//
      itu = TDCoverflow;
      itd = TDCoverflow;
      iqu = ADCuPed + gr->Gaus(0, ADCnoise);
      iqd = ADCdPed + gr->Gaus(0, ADCnoise);
    }
    else {
      itu = tu * TDCuCh2ns;
      itd = td * TDCdCh2ns;
      iqu = qu * ADCuGain + gr->Gaus(ADCuPed, ADCnoise);;
      iqd = qd * ADCdGain + gr->Gaus(ADCdPed, ADCnoise);;

      if(iqu < 0) iqu = 0;//no negative values
      if(iqd < 0) iqd = 0;
    }

    //overflow check
    if(itu > TDCoverflow) itu = TDCoverflow;
    if(itd > TDCoverflow) itd = TDCoverflow;
    if(iqu > ADCoverflow) iqu = ADCoverflow;
    if(iqd > ADCoverflow) iqd = ADCoverflow;

  //digitization
    itu = Int_t(itu);
    itd = Int_t(itd);
    iqu = Int_t(iqu);
    iqd = Int_t(iqd);

   //difference in amplitude before and after digitization.
    diff = tu - itu;

    opt -> Fill();

  }
  // 将数据写入root文件中
  opt->Write();
  opf->Close();

}
In [1]:
%jsroot on
In [2]:
!ls -lh treeADC.*

-rw-r--r--  1 zhli  staff   5.5K Feb 26 16:38 treeADC.C
-rw-r--r--  1 zhli  staff   4.8K Feb 26  2023 treeADC.C~
-rw-r--r--  1 zhli  staff    61M Feb 26 16:40 treeADC.root
In [3]:
TFile *ipf = new TFile("treeADC.root");
In [4]:
TCanvas *c1 = new TCanvas();
c1->Clear();

TDC 分析¶

将多个图画到一张画布上。¶

  • 将多个histogram叠加到一张图上显示的方法，用Draw(“same”)选项， y轴的大小取决于第一个图的范围。
In [5]:
tree->Draw("itu>>htu(420,0,4200)");
TH1D *htu = (TH1D*) gROOT->FindObject("htu");//得到histogram的指针，通过指针进行进一步操作。
tree->Draw("itd>>htd(420,0,4200)");
TH1D *htd = (TH1D*) gROOT->FindObject("htd");
htd->SetLineColor(kGreen);
htu->Draw();
htd->Draw("same");
c1->Draw();

THStack 方法¶

  • 将多个histogram叠加到一张图上显示的方法-II, 自动调整每张图的y轴显示范围。
In [6]:
THStack *hs = new THStack("hs","test stacked histograms");
hs->Add(htu);
hs->Add(htd);
hs->Draw("nostack");//替换成hs->Draw();语句，观察效果。
c1->Draw();
In [7]:
//二维关联图
tree->Draw("itu:itd>>(500,0,5000,500,0,5000)","","colz");//加入pid条件观察图的变化，结合实验设置理解图中不同区域的含义。
gPad->SetLogz();
gPad->SetLogy(0);
c1->Draw();//* 在ROOT环境下可省略

TDC条件的运用¶

In [8]:
//位置分布
tree->Draw("itu-itd");
c1->Draw();//结果是否正常？如果异常，问题出在哪里？

选择参数的有效值范围¶

In [9]:
tree->Draw("itu-itd>>hix(1750,-1250,500)","itu<4095 && itd<4095");
gPad->SetLogy(0);
c1->Draw();

TDC 的显示问题¶

In [10]:
tree->Draw("itu-itd>>(1500,-1250,500)","itu<4095 && itd<4095");//TDC 道值
gPad->SetLogy(0);
c1->Draw();//显示异常
In [11]:
tree->Draw("itu-itd>>(1800,-1250,500)","itu<4095 && itd<4095");//TDC 道值
gPad->SetLogy(0);
c1->Draw();//显示异常

思考题¶

对比上面3个图，尝试解释产生上述现象的原因。

  • 我们将在第二章讨论这个问题，并给出解决方案

QDC分析¶

  • 计算ped峰参数，确定噪声阈值
  • THStack
In [12]:
tree->Draw("iqu>>hquall(420,0,4200)");
TH1D *hquall = (TH1D*)gROOT->FindObject("hquall");
hquall->SetLineColor(kBlack);

tree->Draw("iqu>>hqu0(420,0,4200)","pid==0");
TH1D *hqu0 = (TH1D*)gROOT->FindObject("hqu0");
hqu0->SetLineColor(kGray);

tree->Draw("iqu>>hqu1(420,0,4200)","pid==1");
TH1D *hqu1 = (TH1D*)gROOT->FindObject("hqu1");
hqu1->SetLineColor(kRed);

tree->Draw("iqu>>hqu2(420,0,4200)","pid==2");
TH1D *hqu2 = (TH1D*)gROOT->FindObject("hqu2");
hqu2->SetLineColor(kGreen);

tree->Draw("iqu>>hqu3(420,0,4200)","pid==3");
TH1D *hqu3 = (TH1D*)gROOT->FindObject("hqu3");
hqu3->SetLineColor(kBlue);
THStack *hsqu = new THStack("hsqu","qu with different pid");
In [13]:
hsqu->Add(hquall);
hsqu->Add(hqu0);
hsqu->Add(hqu1);
hsqu->Add(hqu2);
hsqu->Add(hqu3);
hsqu->Draw("nostack");
auto legend = new TLegend(0.7, 0.7, .9, .9);
   legend->SetHeader("qu with different PID","C"); // option "C" allows to center the header
   legend->AddEntry(hquall,"Qu all","l");
   legend->AddEntry(hqu0,"qu for gamma","l");
   legend->AddEntry(hqu1,"qu for neutron","l");
   legend->AddEntry(hqu2,"qu for LP","l");
   legend->AddEntry(hqu3,"qu for pedal","l");
   legend->Draw();
c1->Draw();//辨认pedal峰，超界位置。
In [14]:
tree->Draw("iqd>>hqdall(420,0,4200)");
TH1D *hqdall = (TH1D*)gROOT->FindObject("hqdall");
hqdall->SetLineColor(kBlack);
In [15]:
hqdall->Draw();
c1->Draw();//辨认pedal峰，超界位置

拟合ped峰，提取拟合参数¶

In [16]:
hquall->Fit("gaus","","",0,200);
hqdall->Fit("gaus","","",0,200);
c1->Draw();

 FCN=24369.5 FROM MIGRAD    STATUS=CONVERGED     154 CALLS         155 TOTAL
                     EDM=7.75867e-10    STRATEGY= 1  ERROR MATRIX UNCERTAINTY   2.2 per cent
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     4.08911e+04   1.44653e+02   6.84086e-01  -4.58234e-07
   2  Mean         1.43539e+02   4.41192e-02  -2.93312e-05   5.97606e-05
   3  Sigma        1.23599e+01   2.65350e-02  -1.70202e-06  -6.94629e-02
 FCN=32549.3 FROM MIGRAD    STATUS=CONVERGED     152 CALLS         153 TOTAL
                     EDM=5.05671e-09    STRATEGY= 1  ERROR MATRIX UNCERTAINTY   2.0 per cent
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     4.05854e+04   1.48731e+02   5.09152e-01  -1.14507e-06
   2  Mean         1.33566e+02   4.45418e-02  -6.34267e-05  -5.82882e-04
   3  Sigma        1.24327e+01   2.91691e-02  -1.30791e-06  -9.67228e-02

提取拟合结果的方法¶

In [17]:
TF1 *fgaus[2];
Double_t ped[2], sigma[2];//u,d
TString sq[2] = {"qu", "qd"};
In [18]:
fgaus[0] = hquall->GetFunction("gaus");//得到拟合函数的指针
fgaus[1] = hqdall->GetFunction("gaus");
for(int i = 0;i<2;i++) {
    ped[i] = fgaus[i]->GetParameter(1);//得到拟合函数的第二个参数
    sigma[i] = fgaus[i]->GetParameter(2);
    //TString的格式化输出。用法与printf一致。
    TString ss;
    ss.Form("ped_%s = %.2f, sigma_%s = %.2f",sq[i].Data(),ped[i],sq[i].Data(),sigma[i]); 
    cout << ss << endl;
}

ped_qu = 143.54, sigma_qu = 12.36
ped_qd = 133.57, sigma_qd = 12.43
In [19]:
tree->Draw("iqu:iqd>>(420,0,4200,420,0,4200)","","colz");
c1->SetLogz();
c1->SetLogy(0);
c1->Draw();//* 在ROOT环境下可省略

在tree的Draw(" ")内不能直接输入临时定义的动态数据。¶

In [20]:
tree->Draw("iqu-ped[0]:iqd-ped[1]","iqd<4000 && iqu<4000");

Error in <TTreeFormula::Compile>:  Bad numerical expression : "ped[0]"
Info in <TSelectorDraw::AbortProcess>: Variable compilation failed: {iqu-ped[0]:iqd-ped[1],iqd<4000 && iqu<4000}

ROOT命令的“ ”内加入动态数据的方法-TString::Form()¶

In [21]:
//qu,qd减去ped，去掉噪声及超界值，选择合理的取值范围
TString stree,scut;
stree.Form("(iqu-%f):(iqd-%f)>>hsud(500,0,4000,500,0,4000)",ped[0],ped[1]);//在""内加入动态数据的方法
scut.Form("iqu>(%f+3*%f) && iqu<4000 && iqd>(%f+3*%f) && iqd<4000",ped[0],sigma[0],ped[1],sigma[1]);
tree->Draw(stree.Data(),scut.Data(),"colz");
c1->Draw();
cout << "tree: " << stree.Data() << endl;
cout << "cut: " << scut.Data() << endl;

tree: (iqu-143.538700):(iqd-133.566057)>>hsud(500,0,4000,500,0,4000)
cut: iqu>(143.538700+3*12.359888) && iqu<4000 && iqd>(133.566057+3*12.432733) && iqd<4000

设置参数的别名：tree->SetAlias()¶

In [22]:
TString squa,sqda;
squa.Form("iqu-%f",ped[0]);
sqda.Form("iqd-%f",ped[1]);
tree->SetAlias("qua",squa.Data());
tree->SetAlias("qda",sqda.Data());
TString stcut = "itu>0 && itu<4000 && itd>0 && itd<4000";

scut = scut + " && " + stcut;
tree->Draw("itd-itu:log(qua/qda)",scut.Data(),"colz");
c1->SetLogz();
c1->SetLogy(0);
c1->Draw();
In [23]:
tree->Draw("sqrt(qua*qda):(itd+itu)/2>>(500,500,4000,1000,0,4000)",scut.Data(),"colz");
c1->SetLogz();
c1->SetLogy(0);
c1->Draw();