// tree.cc
void tree(){
//常量声明
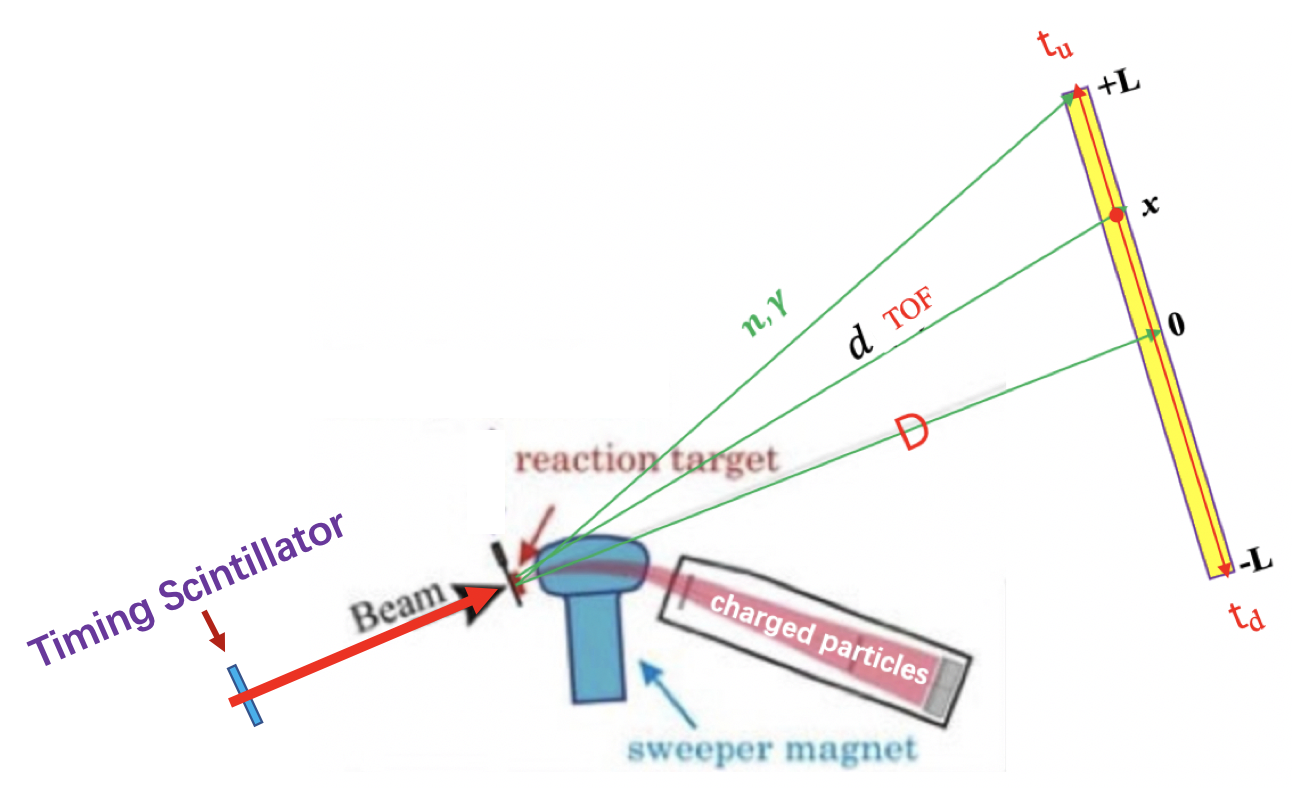
const Double_t D = 500.;//cm, distance between target and the scin.(Center)
const Double_t L = 100.;//cm, half length of the scin.
const Double_t dD = 5.;//cm, thickness of the scin.
const Double_t tRes = 1.;//ns, time resolution(FWHM) of the scintillator.
const Double_t Lambda = 380.;//cm, attenuation lenght of the scin.
const Double_t qRes = 0.1;//relative energy resolution(FWHM) of the scin.
const Double_t Vsc = 7.5;//ns/cm, speed of light in the scin.
const Double_t En0 = 100;//MeV, average neutron energy
const Double_t EnFWHM = 50.;//MeV, energy spread of neutron(FWHM)
const Double_t Eg0 = 1;//MeV, gamma energy
const Double_t RatioGamma = 0.3;//ratio of gamma,ratio of neutron 1-Rg
//1. 声明tree中Branch的变量
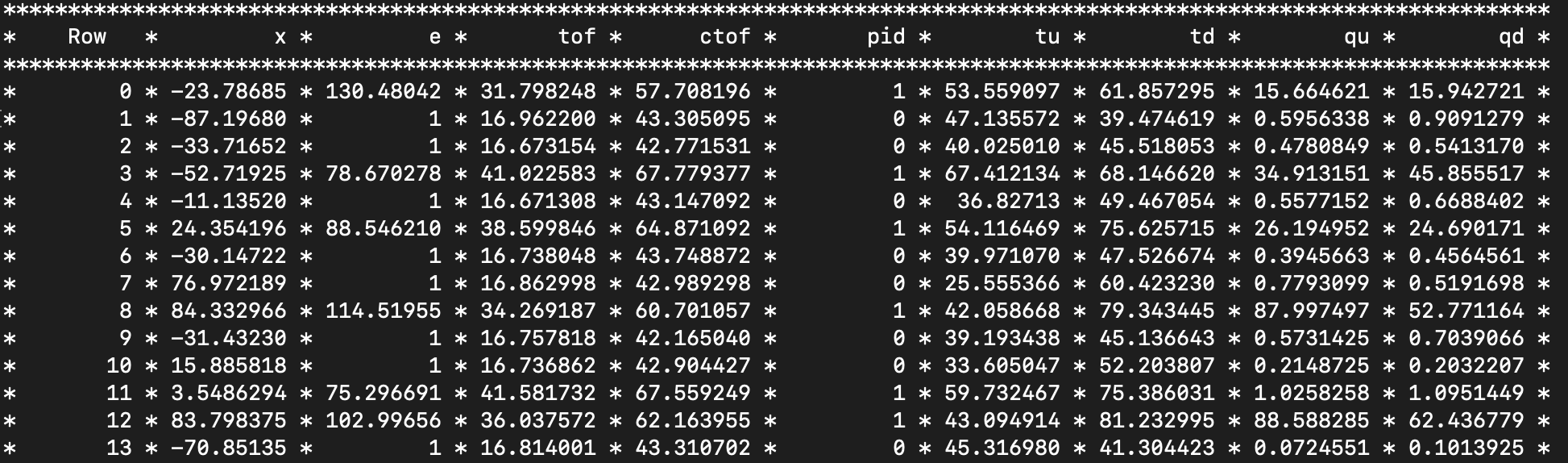
Double_t x;//入射位置
Double_t e;//能量
int pid; //粒子种类,n:pid=1,g:pid=0
Double_t tof, ctof;//TOF:粒子实际飞行时间,cTOF:计算得到的TOF
Double_t tu, td;
Double_t qu, qd;
Double_t tuOff = 5.5;//time offset,
Double_t tdOff = 20.4;//time offset
//2. 定义新ROOT文件,声明新的Tree
TFile *opf = new TFile("tree.root", "recreate");//新文件tree.root,指针 *opf
TTree *opt = new TTree("tree", "tree structure");//新tree,指针 *opt
//3. 将变量地址添加到tree结构中
//第一个参数为变量名称,第二个为上面定义的变量地址,第三个为变量的类型说明,D表示Double_t,I表示 Int_t。
opt->Branch("x", &x, "x/D");
opt->Branch("e", &e, "e/D");
opt->Branch("tof", &tof, "tof/D");
opt->Branch("ctof",&ctof,"ctof/D");
opt->Branch("pid", &pid, "pid/I");
opt->Branch("tu", &tu, "tu/D");
opt->Branch("td", &td, "td/D");
opt->Branch("qu", &qu, "qu/D");
opt->Branch("qd", &qd, "qd/D");
// histogram,ROOT文件中除了TTree结构外,还可存储histogram,graph等
TH1D *hctof = new TH1D("hctof", "neutron time of flight", 1000, 0, 100);
TRandom3 *gr = new TRandom3(0);//声明随机数
//4. 循环,计算变量的值,逐事件往tree结构添加变量值。
for(int i = 0; i < 100000; i++){
x = gr->Uniform(-L, L);//粒子入射位置,在-L,L范围内均匀抽样.
Double_t Dr = D + gr->Uniform(-0.5, 0.5) * dD;//粒子在探测器厚度范围内均匀产生光信号
Double_t d = TMath::Sqrt(Dr * Dr + x * x);//粒子实际飞行距离
if(gr->Uniform() < RatioGamma) { //判断为gamma入射
pid = 0;
e = Eg0;
tof = 3.333 * (d * 0.01);
}
else { //neutron
pid = 1;
e = gr->Gaus(En0, EnFWHM/2.35); // energy of neutrons
tof = 72.29824/TMath::Sqrt(e) * (d * 0.01);//ns
}
if(isnan(tof)) continue; //check ZeroDivisionError
tu = tof + (L - x)/Vsc + tuOff;
tu = gr->Gaus(tu, tRes/2.35);
td = tof + (L + x) / Vsc + tdOff;
td = gr->Gaus(td, tRes/2.35);
ctof = (tu + td)/2.;//simplified calculation.
hctof->Fill(ctof);
//neutron:energy of recoil proton in plas. q0=0-En; gamma:q0=0-Egamma,compton plateau
Double_t Q0 = e * gr->Uniform(); //light response of Qee = f(Ep) is not considered
qu = Q0 *TMath::Exp(-(L - x)/Lambda);
qu = gr->Gaus(qu, qu * qRes/2.35);//QRes, relative energy resolution
qd = Q0 * TMath::Exp(-(L + x)/Lambda);
qd = gr->Gaus(qd, qd * qRes/2.35);
//5.将计算好的变量值填到Tree中
opt->Fill();
if(i%1000 == 0) cout << ".";
}
cout << endl;
// 6.将数据写入root文件中
hctof->Write(); // 将预定义的histogram写到文件
opt->Write(); // 将TTree到文件
opf->Close(); // 关闭文件
}